filmov
tv
Integral 1/1-x^2 two ways

Показать описание
In this video, I compute an antiderivative of 1/(1-x^2) in two ways: 1) Using partial fractions and 2) Using hyperbolic trig substitution. From those two approaches I derive a really cool identity, which shows that you can derive mathematical identities not only using differentiation, but also using integration. Enjoy!
Note: Credit goes to footskills / Zach Lee for coming up with this idea, thank you so much for the suggestion and the main ideas!
Note: Credit goes to footskills / Zach Lee for coming up with this idea, thank you so much for the suggestion and the main ideas!
Integral 1/1-x^2 two ways
Integral 1/x^2 + 1 two ways
Integral of 1/(1+x^2)
the integral of 1/(1-x^2) (hyperbolic functions vs partial fractions?)
how Richard Feynman would integrate 1/(1+x^2)^2
Integral of 1/sqrt(1-x^2)
How REAL Men Integrate Functions
integral of 1/(x^2+1) but you didn't learn it this way in calculus 2
Week12 Open Session (Statistics I)
integral of 1/(1+x^2)^2
How to integrate 1/x^2
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
when calculus students use trig identities too early
Integral of x^2/(1+x^2) two ways
integral battle#10: what? twins?
i did another 100 integrals!
Every Student Should See This
Indefinite Integral of 1/x^2
When mathematicians get bored (ep1)
INTEGRATION IMPORTANT QUESTION | CBSE BOARDS | CLASS 12 MATHS | STATE BOARDS | CUET #shorts_
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
This is a very famous limit
When a calculus teacher says “I will only put 1 integral on the test”
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Комментарии
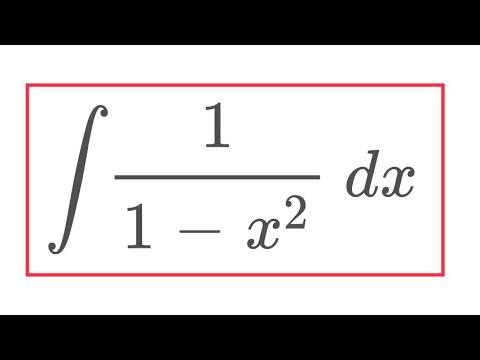 0:12:32
0:12:32
 0:14:41
0:14:41
 0:02:29
0:02:29
 0:08:45
0:08:45
 0:08:53
0:08:53
 0:02:56
0:02:56
 0:00:35
0:00:35
 0:09:21
0:09:21
 2:46:30
2:46:30
 0:06:06
0:06:06
 0:01:07
0:01:07
 0:00:09
0:00:09
 0:00:43
0:00:43
 0:06:50
0:06:50
 0:06:38
0:06:38
 0:00:16
0:00:16
 0:00:58
0:00:58
 0:10:09
0:10:09
 0:00:37
0:00:37
 0:00:33
0:00:33
 0:22:40
0:22:40
 0:00:48
0:00:48
 0:00:18
0:00:18
 0:00:38
0:00:38