filmov
tv
Number Theory | There is a primitive root modulo every power of an odd prime!!

Показать описание
We prove that for an odd prime p, there is a primitive root modulo p^n for all natural numbers n.
Algebraic number theory - an illustrated guide | Is 5 a prime number?
The Alternate Math Universe Where Infinity is Tiny
The High Schooler Who Solved a Prime Number Theorem
The foundation -- Number Theory 1
Number Theory | Divisibility Basics
The Math Needed for Computer Science (Part 2) | Number Theory and Cryptography
Top ten open problems in Number Theory
The Most Efficient Way for Beginners to Start Understanding Number Theory!
First Course in Number Theory | Lecture 3.5 Applications of Bezout's Theorem
Number Theory: The Division Algorithm
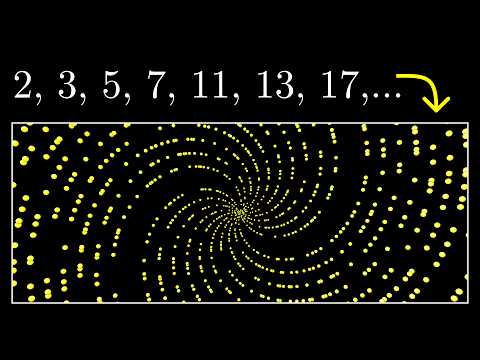
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
How to Learn Number Theory
Number Theory | Linear Congruence Example 2
The bridge between number theory and complex analysis
A number theory proof
Andrew Granville - 1/3 The pretentious approach to analytic number theory
Number Theory: Queen of Mathematics
Greek number theory (a) | Math History | NJ Wildberger
Number Theory | The GCD as a linear combination.
A nice and quick elementary number theory problem.
Pi hiding in prime regularities
Jeffrey Harvey - From Moonshine to Black Holes: Number Theory in Math and Physics (Sept 6, 2017)
Is math discovered or invented? - Jeff Dekofsky
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Комментарии
 0:20:31
0:20:31
 0:33:06
0:33:06
 0:05:15
0:05:15
 0:19:53
0:19:53
 0:07:13
0:07:13
 0:08:08
0:08:08
 0:06:35
0:06:35
 0:02:29
0:02:29
 0:26:55
0:26:55
 0:12:49
0:12:49
 0:22:21
0:22:21
 0:02:59
0:02:59
 0:04:44
0:04:44
 0:09:59
0:09:59
 0:10:17
0:10:17
 1:08:49
1:08:49
 1:02:35
1:02:35
 0:42:04
0:42:04
 0:11:29
0:11:29
 0:09:44
0:09:44
 0:30:42
0:30:42
 0:55:52
0:55:52
 0:05:11
0:05:11
 0:22:09
0:22:09