filmov
tv
How to evaluate for the half angle of tangent
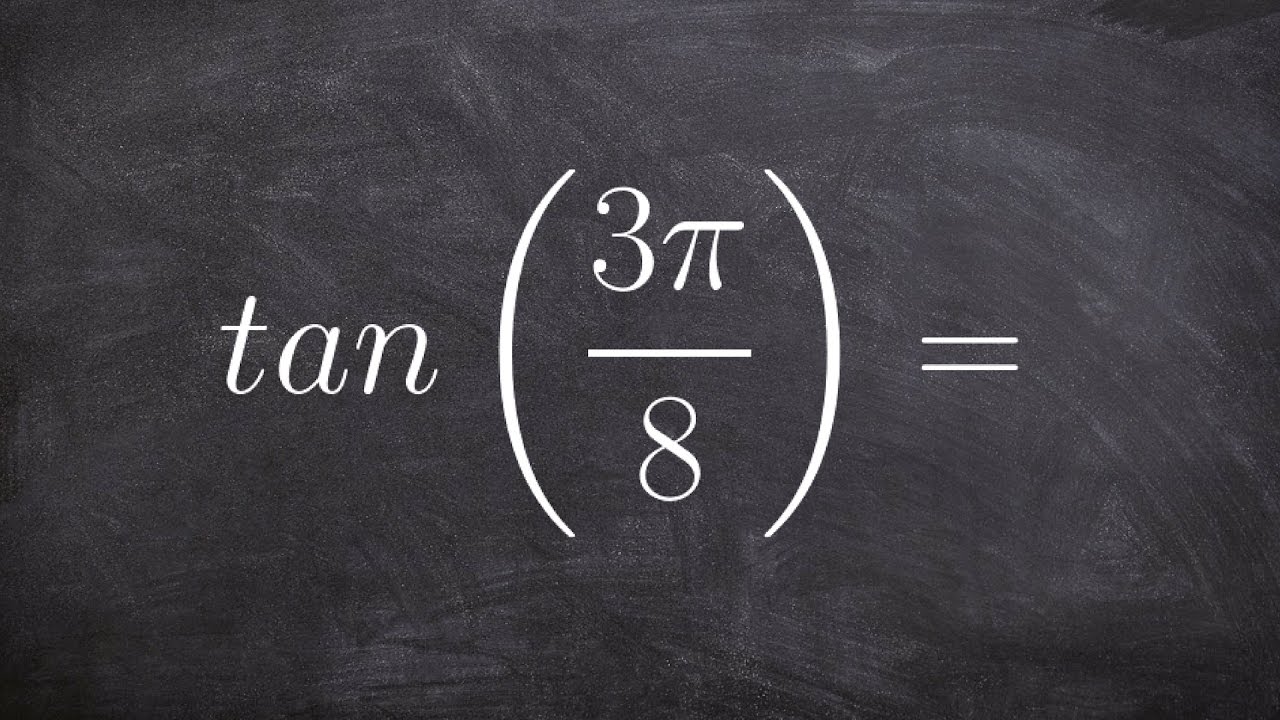
Показать описание
👉 Learn how to evaluate the Sine of an angle using the half-angle formula. The half-angle formula for Sine is helpful when you need to determine the exact value of function given an angle but cannot use a calculator or the angle is not on the unit circle. To evaluate all we need to do is enter the angle into the formula and simplify. Rationalizing the denominator is not required but often is asked to be performed.
Organized Videos:
✅ Half Angle Formulas
✅ Evaluate Half Angle Formulas of and Angle
✅ Evaluate Half Angle Formulas from a triangle
✅ Write the Expression as a single function | Half Angle Formulas
✅ Solve Equations using Half Angle Formulas
Connect with me:
#analytictrig #brianmlogan
Organized Videos:
✅ Half Angle Formulas
✅ Evaluate Half Angle Formulas of and Angle
✅ Evaluate Half Angle Formulas from a triangle
✅ Write the Expression as a single function | Half Angle Formulas
✅ Solve Equations using Half Angle Formulas
Connect with me:
#analytictrig #brianmlogan
Learn how to evaluate for a function
How to evaluate for the composition of the tangent and cosine
How to evaluate for a value the product of two functions
How to evaluate for the cosine of an angle using the sum formula
How to evaluate for the secant of an angle without using a calculator
How to evaluate a piecewise function
How to Evaluate Functions
How to use period as an aide to evaluate for the tangent function of an angle
How to Build Your First AI Model
How to Evaluate Functions? Evaluating Function - General Mathematics
How to evaluate for the composition of two trigonometric functions
Learn how to evaluate for the secant of - 150 degrees
Learn how to evaluate for the secant of a negative angle using the unit circle
How to use the difference of two angles to evaluate for the sine of an angle
How to evaluate for three different values of a piecewise function
Learn how to evaluate a function for a given value
Intro to Evaluating Algebraic Expressions | How to Evaluate Algebraic Expressions | Math with Mr. J
Algebraic Expressions Made Easy: Learn How to Evaluate Them
How to evaluate for the half angle of tangent
How to evaluate VC offers 🤔
Tutorial for how to evaluate for the composition of two trigonometric functions
How to evaluate a function for a given value
How to evaluate for the cosine of an angle using the half angle formula
Evaluate People By What They Do, Not What They Say I Robert Greene
Комментарии
 0:02:15
0:02:15
 0:03:49
0:03:49
 0:02:23
0:02:23
 0:03:50
0:03:50
 0:03:48
0:03:48
 0:00:40
0:00:40
 0:03:16
0:03:16
 0:02:51
0:02:51
 0:00:20
0:00:20
 0:06:52
0:06:52
 0:07:10
0:07:10
 0:03:26
0:03:26
 0:02:37
0:02:37
 0:04:10
0:04:10
 0:02:04
0:02:04
 0:01:42
0:01:42
 0:05:32
0:05:32
 0:00:53
0:00:53
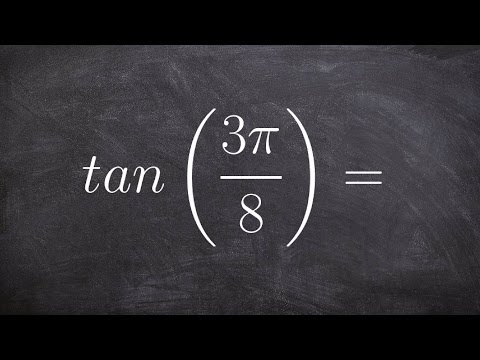 0:03:21
0:03:21
 0:00:19
0:00:19
 0:04:46
0:04:46
 0:01:10
0:01:10
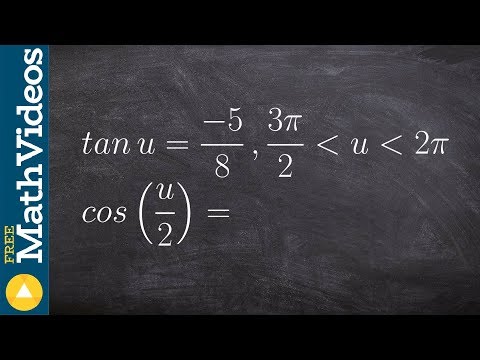 0:04:23
0:04:23
 0:00:55
0:00:55