filmov
tv
An interesting trigonometry problem -- featuring roots of unity.

Показать описание
We present a derivation of a pretty classic trigonometric identity that involves multiples of pi/11.
This is adapted from a solution in the Problems and Solutions section of the September 2006 issue of The College
Mathematics Journal.
This is adapted from a solution in the Problems and Solutions section of the September 2006 issue of The College
Mathematics Journal.
An interesting trigonometry problem -- featuring roots of unity.
Fun trigonometry problem
And You Thought Trigonometry Was Pointless…
A Trigonometry Problem JEE Advanced
Interesting Trigonometry Problem | cos(sinx)=1/2
How To Solve Two Triangle Trigonometry Problems
Learn How To Prove A Trigonometry Question & Apply Trig Identities Effectively
Random Math Problem 1: Trigonometry
Derivative of trigonometric functions ( thomas calculus)
Solve Trigonometry in 10 Seconds | IIT JEE Short Cuts & Tricks | JEE Main 2021 | Score Quick Mar...
#Trigonometry all formulas
❖ Trigonometry Word Problem, Finding The Height of a Building, Example 1 ❖
Trigonometry - Real Life Applications
Trigonometry For Beginners!
Trigonometry Practice Problems
Trick for doing trigonometry mentally!
Trigonometry Funny😂😂😂😂 | #shorts #relatable #cbse #class11 #class12 #class10 #jee
Trigonometry Concepts - Don't Memorize! Visualize!
Ferris Wheel Trigonometry Problem
Trigonometry Word Problem, Determining the Speed of a Boat, Example 3
Trigonometry identity review/fun | Trig identities and examples | Trigonometry | Khan Academy
Important problem of Trigonometry | General Solution Of sin^100 x + cos^100 x = 1
Trigonometry Class 10 | Trigonometry Identities| Trigonometry Formulas #fun #shorts #youtubeshorts
The Hardest Math Test
Комментарии
 0:25:21
0:25:21
 0:01:00
0:01:00
 0:01:00
0:01:00
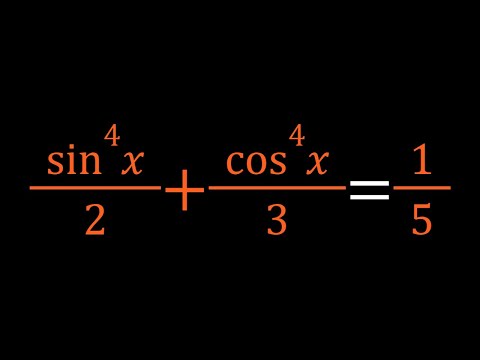 0:09:15
0:09:15
 0:00:49
0:00:49
 0:15:14
0:15:14
 0:13:17
0:13:17
 0:10:59
0:10:59
 0:00:59
0:00:59
 0:32:33
0:32:33
 0:00:16
0:00:16
 0:07:31
0:07:31
 0:40:27
0:40:27
 0:21:52
0:21:52
 0:06:31
0:06:31
 0:05:02
0:05:02
 0:00:31
0:00:31
 0:32:35
0:32:35
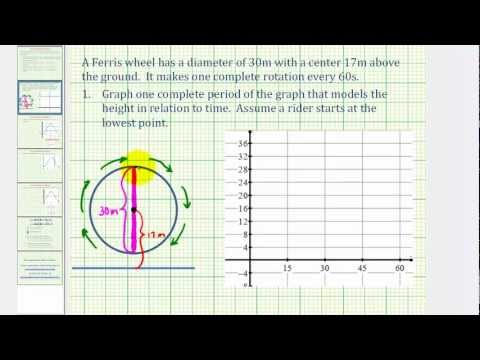 0:13:34
0:13:34
 0:08:28
0:08:28
 0:11:07
0:11:07
 0:09:06
0:09:06
 0:00:14
0:00:14
 0:00:28
0:00:28