filmov
tv
A strange sequence
Показать описание
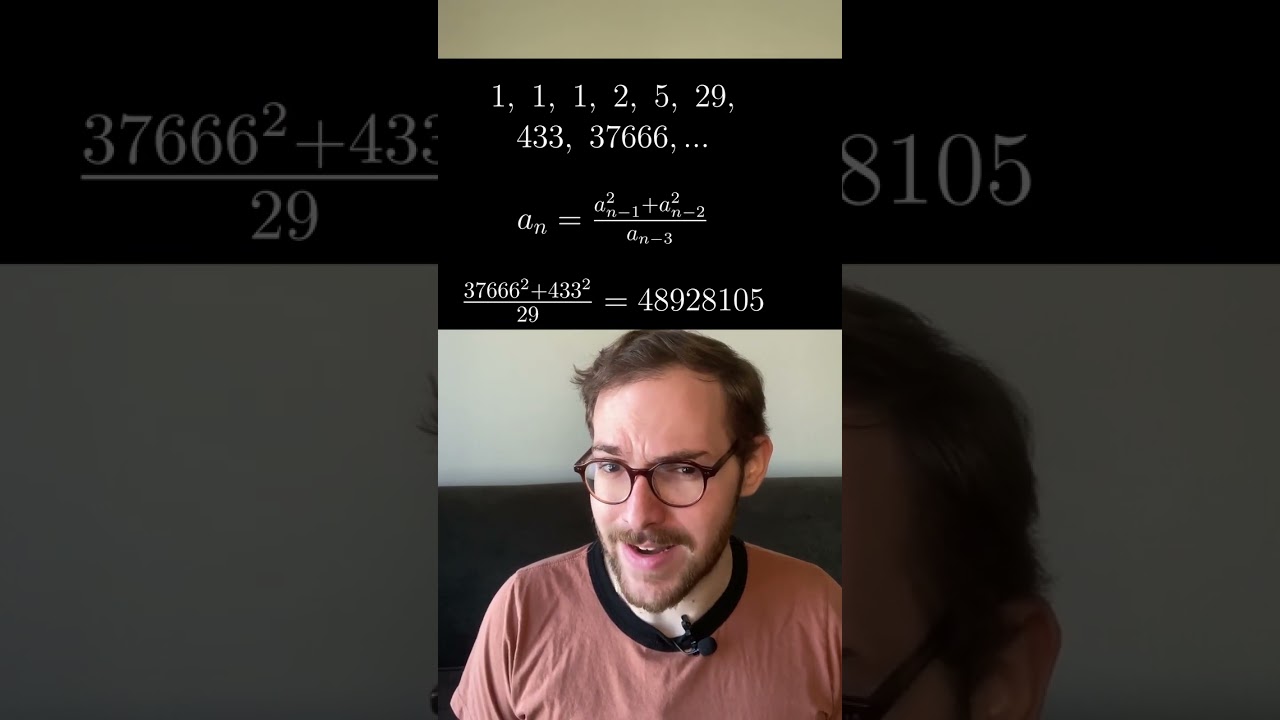
This is an example of the Laurent phenomenon, a somewhat recently discovered pattern in combinatorics.
A strange sequence
Something Strange Happens When You Keep Squaring
Mick Jagger - Strange Game (Official Lyric Video)
Strange Multiplication: Sequence Contraction and Sequence Sequencing
Doctor Strange - Open your eye (custom edit, 4K, re-colored)
A Very Strange Sequence
A Strange Sequence Of Circumstance
why Dr Strange lie about 14,000,605 possibilities #shorts
Marvel Rivals new team up ‘Arcane Order’ Scarlet Witch & Doctor Strange
Antonio Damasio, What is the strange order of things?
I loved then HATED the Doctor Strange in the Multiverse of Madness ending
Zombie Strange vs. The Scarlet Witch Fight Scene [No BGM|Doctor Strange in the Multiverse of Madness
The Scarlet Witch vs. The Illuminati Fight Scene [No BGM] | Dr. Strange in the Multiverse of Madness
Ranking Every Life is Strange Female Love Interest [2025 Edition] 🔥
Strange Sequences / Lost Frequencies
Ebony Maw Tortures Doctor Strange Scene | AVENGERS: INFINITY WAR (2018) Movie CLIP HD
After creating a strange sequence, the whole world regrets betraying me
R RATED DR Strange 2 Scarlet Witch DELETED SCENE
Did you know that in 'DOCTOR STRANGE 2'...
Doctor Strange in the Multiverse of Madness - Extended Preview (2022) | Vudu
Strange Sequence
New Order vs. Depeche Mode - Strange Love Triangle (Remastered Remix)
Max Caulfield's New Outfits 🔥🔥 (Life is Strange Double Exposure)
DOCTOR STRANGE SAVED LITTLE BOY || ATTITUDE WHATSAPP STATUS 🔥
Комментарии
 0:00:23
0:00:23
 0:33:06
0:33:06
 0:03:32
0:03:32
 0:04:20
0:04:20
 0:04:05
0:04:05
 0:00:42
0:00:42
 0:04:31
0:04:31
 0:00:59
0:00:59
 0:00:09
0:00:09
 0:05:25
0:05:25
 0:00:32
0:00:32
 0:04:02
0:04:02
 0:04:24
0:04:24
 0:00:30
0:00:30
 0:10:27
0:10:27
 0:05:43
0:05:43
 21:31:37
21:31:37
 0:00:43
0:00:43
 0:00:43
0:00:43
 0:07:37
0:07:37
 0:05:16
0:05:16
 0:06:51
0:06:51
 0:00:12
0:00:12
 0:00:35
0:00:35