filmov
tv
Symmetric derivative of abs(x) at 0

Показать описание
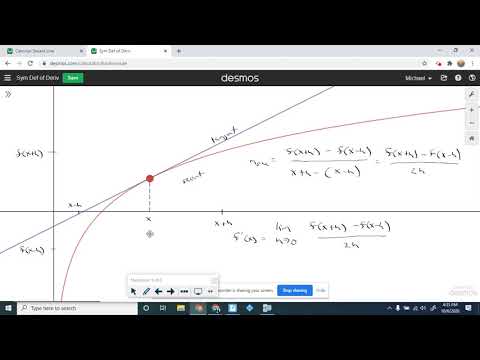
Have you ever felt sad that we do not have a derivative of abs(x) at 0?
If so, then try symmetric derivative!
------------------------------------------------------------------------------------
------------------------------------------------------------------------------------
bprp fast
If so, then try symmetric derivative!
------------------------------------------------------------------------------------
------------------------------------------------------------------------------------
bprp fast
Symmetric derivative of abs(x) at 0
symmetric derivative
Derivative of x+abs(x)
symmetric derivative
Symmetric Definition of the Derivative
Derivative of abs(x^2 -6x +5)
Derivative of abs(x) by definition #maths
Lesson 3.2 Video 4 - Applying the Symmetric Difference Quotient to Approximate a Derivative
derivative of mod(x) at x=0.Derivative of absolute value function at x=0.
Symmetry of the second derivative (when continuous)
Derivative of y = ln|x| or natural log of absolute value of x
How REAL Men Integrate Functions
Derivatives using the limit definition symmetric difference Calculus AP calc derivative
Derivative of Inverse Secant and Why the Absolute Value?
How to Differentiate Absolute Value of x | Differentiation Of Modulus x | Derivative of |x|
Functions y = abs(x)
260 - [ENG] derivative of xT A x quadratic form
A New Definition of the Derivative? #SoME3
Difference Between Partial and Total Derivative
33 Derivative of Absolute Quadratice Function Graph
Derivative of Absolute Value Function Using the Limit Definition
The derivative of `f(x)=|x|^(3) at x=0` does / is-
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
12Adv Part 1 Multiple Choice | MCQ | EoT1 | Limits, derivative, continuity, trig | Q1-Q15 | 12A |
Комментарии
 0:01:45
0:01:45
 0:13:09
0:13:09
 0:04:09
0:04:09
 0:01:12
0:01:12
 0:11:08
0:11:08
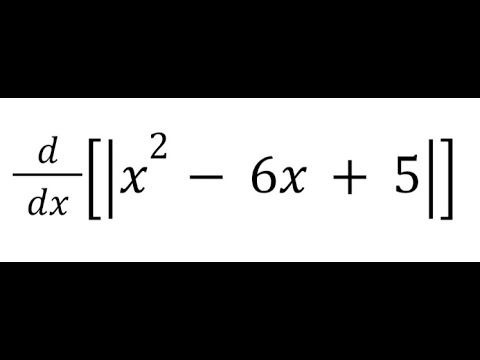 0:01:43
0:01:43
 0:00:56
0:00:56
 0:01:28
0:01:28
 0:14:35
0:14:35
 0:24:44
0:24:44
 0:05:36
0:05:36
 0:00:35
0:00:35
 0:25:14
0:25:14
 0:17:13
0:17:13
 0:03:15
0:03:15
 0:06:34
0:06:34
![260 - [ENG]](https://i.ytimg.com/vi/oO5c3KNPnK0/hqdefault.jpg) 0:02:56
0:02:56
 0:23:50
0:23:50
 0:01:44
0:01:44
 0:12:30
0:12:30
 0:06:18
0:06:18
 0:02:21
0:02:21
 0:00:12
0:00:12
 2:54:29
2:54:29