filmov
tv
Limit of x^(1/lnx) as x approaches infinity

Показать описание
In this video we find the limit of of (tanx/x)^1/x^2 as x approaches 0 using L'Hopitals rule. Each step is explained carefully. Limit Laws are taken for granted in this problem.
If you found this content useful, make sure to SUBSCRIBE and check out some of my other videos! Thanks for watching I hope you have a great day. All questions are welcome.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
If you found this content useful, make sure to SUBSCRIBE and check out some of my other videos! Thanks for watching I hope you have a great day. All questions are welcome.
I have linked some videos below which I think you may find useful! If you are struggling on this topic make sure to check them out!
Limit of x^x^x as x goes to 0+ :
Limit of (1+1/x)^x as x approaches infinity :
Limit of (x/x+a)^x as x approaches infinity :
Limit of x^x as x goes to 0+ :
I hope you have a great day!
Limit of x^(1/lnx) as x approaches infinity
Limit of (x^(x-1) - 1/x)/lnx as x→0+
Limit of lnx/x as x goes to Infinity (L'Hospital's Rule) | Calculus 1 Exercises
Limit of x*lnx as x approaches 0 (L'Hospital's Rule) | Calculus 1 Exercises
Calculus Help: Find the limits: Lim {x approaches 1+ } (1/lnx - 1/(x-1)) - L'Hospital - Derivat...
limit of 1/lnx - 1/(x-1) as x goes to 1 Using L'Hôpital's rule
Limit of (ln(x+1)/lnx)^xlnx as x approaches +infinity 😍😍
limit of x-ln(x) as x goes to infinity via L'Hospital's Rule
Boğaziçi Üniversitesi Math101 Spring 2013 İkinci Midterm
`lim_(x- gtoo)(xln(1+(lnx)/x))/(lnx)`
Evaluate the limit as x approaches infinity for (ln(2x) - ln(x+1)). l’Hopital’s Rule
Solve the Limit of (x - lnx) as x goes to Infinity Using L'Hopitals Rule
Limit of lnx as x approaches 0 | Real Analysis Exercises
Find the limit as x approaches 1^+ for (ln x tan(pi x/2)) l’Hopital’s Rule
L'hopital's rule
Evaluate the limit as x approaches 0^+ for (x ln x). l’Hopital’s Rule
limit as x approaches infinity of x^(ln2/(1+lnx)). No L'Hospital's Rule
limit of lnx/(x-1) as x approaches 1 Using L'Hôpital's rule
L’HOSPITAL'S RULE | Limit of ln(x)/sqrt(x) as x goes to infinity | JAKE'S MATH LESSONS
find limit of (lnx-1)/(x-e) when x tends to e.
Calcule de limite très simple x^(1/lnx)
limit x approaches 1 from the right of 1/lnx - 1/(x-1)
Proof: the derivative of ln(x) is 1/x | Advanced derivatives | AP Calculus AB | Khan Academy
How to use L'Hopital's Rule to Find the Limit of ln(ln(x))/x as x approaches Infinity #sho...
Комментарии
 0:01:25
0:01:25
 0:02:21
0:02:21
 0:02:21
0:02:21
 0:03:35
0:03:35
 0:04:09
0:04:09
 0:06:39
0:06:39
 0:05:01
0:05:01
 0:03:02
0:03:02
 1:05:51
1:05:51
 0:03:04
0:03:04
 0:02:07
0:02:07
 0:02:30
0:02:30
 0:03:36
0:03:36
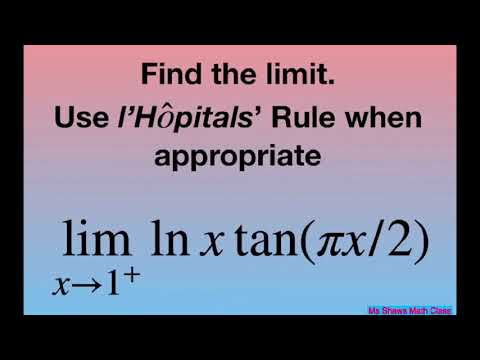 0:02:48
0:02:48
 0:13:09
0:13:09
 0:02:18
0:02:18
 0:01:19
0:01:19
 0:10:38
0:10:38
 0:05:02
0:05:02
 0:12:50
0:12:50
 0:01:59
0:01:59
 0:02:08
0:02:08
 0:08:08
0:08:08
 0:00:43
0:00:43