filmov
tv
limit of x-ln(x) as x goes to infinity via L'Hospital's Rule

Показать описание
limit of x-ln(x) as x goes to infinity via L'Hospital's Rule. This is an indeterminate form of infinity - infinity so we must "do more work"! If you know my secret weapon, The List, then you can say that x will be so much bigger than ln(x) as x goes to infinity, so much bigger so that x-ln(x) is infinity. But this calculus 1 tutorial shows you why it is true.
Use "WELCOME10" for 10% off
Subscribe for more calculus tutorials 👉 @bprpcalculusbasics
-------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
-------------------
😊 Thanks to all channel members 😊
Sandglass Dªrksun Seth Morris Andrea Mele
---------------------------------------------------------
---------------------------------------------------------
Best wishes to you,
#justcalculus
Use "WELCOME10" for 10% off
Subscribe for more calculus tutorials 👉 @bprpcalculusbasics
-------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie (10% off with the code "WELCOME10"):
-------------------
😊 Thanks to all channel members 😊
Sandglass Dªrksun Seth Morris Andrea Mele
---------------------------------------------------------
---------------------------------------------------------
Best wishes to you,
#justcalculus
limit of x-ln(x) as x goes to infinity via L'Hospital's Rule
Limit xln(x) as x approaches 0 from right, done in 2 minutes!
Limit of x*lnx as x approaches 0 (L'Hospital's Rule) | Calculus 1 Exercises
Limit of ln(x+lnx)/x as x approaches infinity
L’HOSPITAL'S RULE | Limit of ln(x)/sqrt(x) as x goes to infinity | JAKE'S MATH LESSONS
Limit of (x /ln(x)) as x approaches infinity
Limit of lnx/x as x goes to Infinity (L'Hospital's Rule) | Calculus 1 Exercises
How to use L'Hopital's Rule to Find the Limit of ln(ln(x))/x as x approaches Infinity #sho...
limit of x*ln(x) as x approaches 0
Approaching Zero: Understanding the Behavior of ln(x) as x Gets Infinitely Small
lim[x-» ∞] (x - ln(x))
Explain using limits which function grows faster f(x) = ln x or g(x) = sqrt(x).
Limit of ln(x+1)/ln(x) WITHOUT using L'Hopital's Rule or Negligibility / Insignificant Sho...
Evaluate the limit as x approaches 0^+ for (x ln x). l’Hopital’s Rule
Find limit as x approaches 3 of ln (x^2 -9) and lim as x approaches infinity of [ln(2+x) - ln(1+x)]
Find the limit as x approaches infinity for (x - ln x). l’Hopital’s Rule
Limit of 1/ln(x)
Limits of Natural Logarithmic Functions - Calculus
Limit of ln(x+1)/ln(x) WITHOUT using L'Hopital's Rule or Negligibility / Insignificant Sho...
Finding a Limit Using L'Hopital's Rule e^(-x)*ln(x) as x approaches infinity
Find the limit as x approaches 0^+ for ln x/x. Use l’Hospitals’ Rule if appropriate
why integral of 1/x gives ln(x)+C #apcalculus
a harder L'Hospital's rule problem, limit of x/(x-1)-1/ln(x) as x goes to 1, calculus tuto...
Find the limit as x approaches 0^+ for sin x ln x. l’Hopitals’ Rule
Комментарии
 0:03:02
0:03:02
 0:01:56
0:01:56
 0:03:35
0:03:35
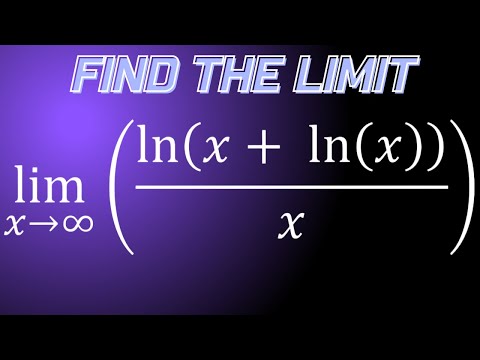 0:03:02
0:03:02
 0:05:02
0:05:02
 0:01:58
0:01:58
 0:02:21
0:02:21
 0:00:43
0:00:43
 0:05:32
0:05:32
 0:00:50
0:00:50
![lim[x-» ∞] (x](https://i.ytimg.com/vi/XVtAVyDGUrY/hqdefault.jpg) 0:05:46
0:05:46
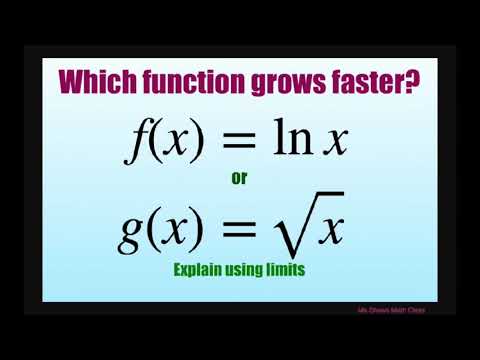 0:03:22
0:03:22
 0:00:36
0:00:36
 0:02:18
0:02:18
 0:05:15
0:05:15
 0:02:14
0:02:14
 0:00:13
0:00:13
 0:14:18
0:14:18
 0:02:04
0:02:04
 0:01:39
0:01:39
 0:02:29
0:02:29
 0:00:34
0:00:34
 0:04:33
0:04:33
 0:03:32
0:03:32