filmov
tv
Теория вероятностей #11: формула полной вероятности, формула Байеса

Показать описание
Что такое формула полной вероятности. Вывод формулы Байеса и примеры ее использования.
Теория вероятностей #11: формула полной вероятности, формула Байеса...
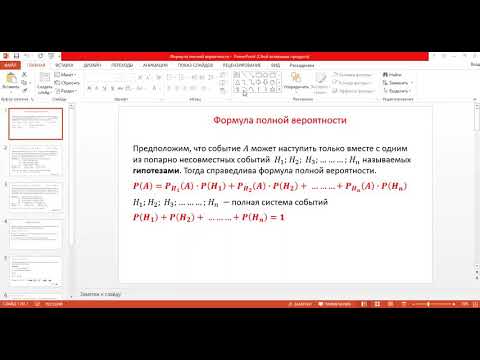
Формула полной вероятности. Формула Байеса.
✓ Формула Байеса в реальной жизни | Математика вокруг нас | Борис Трушин...
08 Формула полной вероятности Задачи
Формула полной вероятности. Формула Байеса
Формула полной вероятности. Формула Байеса
Теория вероятностей | Математика TutorOnline
Формула полной вероятности.
Формула Байеса. Какова вероятность болезни?
Формулы полной вероятности и Байеса
формула полной вероятности, формула
06 Формула полной вероятности ЗадачиОИС
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛЫ БАЙЕСА
Вся теория вероятностей для экзамена за 20 минут. ЕГЭ профильный, Базовый, ОГЭ...
Формула полной вероятности. Когда лучше заходить на экзамен?...
ТВ-4. Формула полной вероятности. Теорема Байеса
ТВ Формула полной вероятности Формула Байеса
Формула полной вероятности. Формула Байеса.
Теория вероятностей. Формула полной вероятности.
17.3 формула полной вероятности - доказательство формулы...
Формула полной вероятности на конкретных примерах. №5 ЕГЭ профиль...
Формула полной вероятности и формула Байеса
Формула полной вероятности
Формула полной вероятности. Формула Байеса (1)
Комментарии
 0:07:19
0:07:19
 0:27:27
0:27:27
 0:09:39
0:09:39
 0:25:52
0:25:52
 0:42:51
0:42:51
 0:10:10
0:10:10
 0:09:04
0:09:04
 0:09:47
0:09:47
 0:05:41
0:05:41
 0:39:21
0:39:21
 0:20:57
0:20:57
 0:31:00
0:31:00
 0:20:09
0:20:09
 0:19:45
0:19:45
 0:04:07
0:04:07
 1:35:48
1:35:48
 0:13:43
0:13:43
 0:13:30
0:13:30
 0:08:07
0:08:07
 0:05:17
0:05:17
 0:13:05
0:13:05
 0:15:34
0:15:34
 1:38:36
1:38:36
 0:08:12
0:08:12