Circular velocity and acceleration with geometric algebra

In this video, the geometric algebra form for the circular unit vectors will be derived, and then used to compute expressions for velocity and acceleration in a circular coordinate system.

This video includes a very brief introduction to (2D) geometric algebra, including the exponential form for a 2D rotation. Specifically, this video includes:

* A reminder of what circular coordinates are.
* A brief outline of what is meant by each of the circular basis vectors.
* A derivation of those basis vectors (just basic geometry, and no GA.)
* A brief introduction to geometric algebra, and geometric algebra for a plane, including the "imaginary" i = e_1 e_2, and it's use for rotation and polar form.
* How to express the circular basis vectors in polar form.
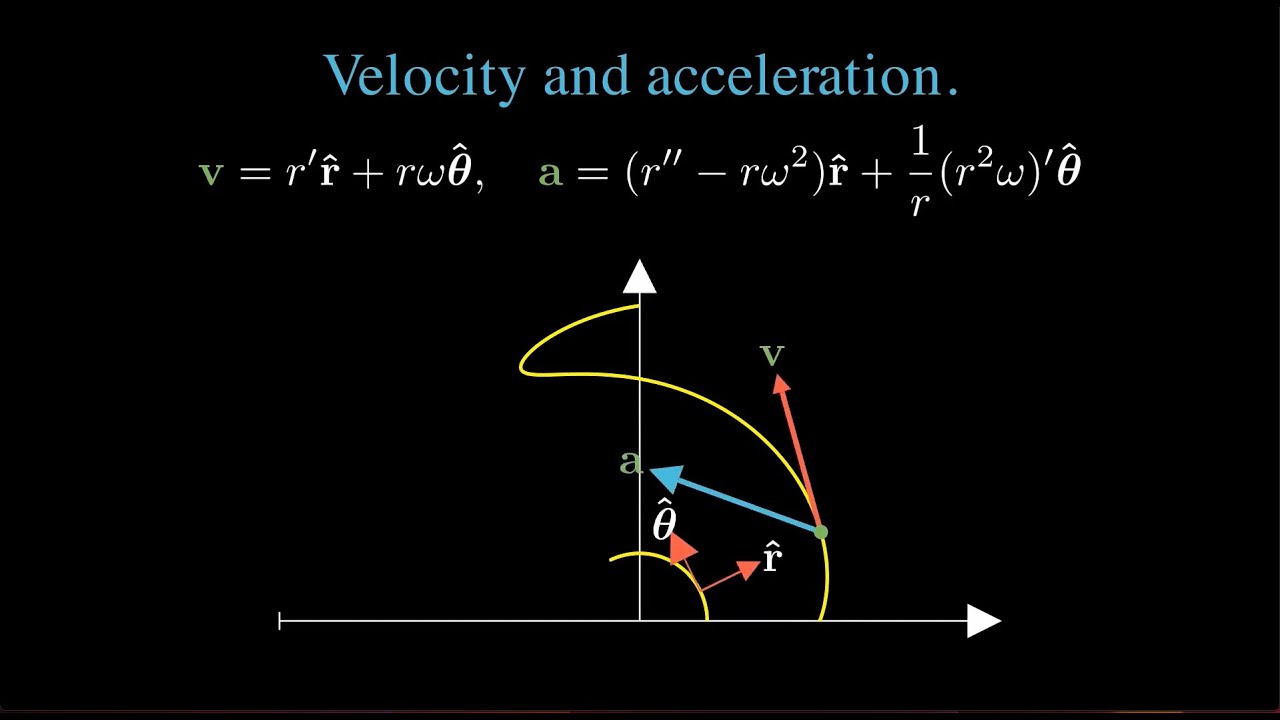
* Application of all the ideas above to compute velocity and acceleration.
* Circular coordinate examples of velocity and acceleration.

Prerequisites: calculus (derivatives and chain rule), complex numbers (exponential polar form), and basic vector algebra (basis, vector space, dot product space, arrow representation of vectors, graphical vector addition, ...)

If you liked this video, you may be interested in my book, Geometric Algebra for Electrical Engineers, available in hardcover or softcover on amazon:

An electronic (PDF) version of the book is available on my blog here:

[SirTravelMuffin]

Thank you for such a great demonstration of the power of GA!

[OmnipotentJC]

This was a very informative and well put together video. Thank you!

[minimath]

Awesome video! I find unfortunate that the convention for unit vectors are e1 and e2 because e the transcendental numbers shows up next it. It can be a little confusing but you did distinguished between them italicizing the e.

[rainbow-clrk]

Really good vidéo !
It's a little bit odd to use GA for this problem since you can do all the thing you have done with complexe numbers or matrices. I know it's equivalent since one can draw an isomorphism but it feels you use GA only for the sake of using it.
The animation are really well done, congratulations 👏

[SillySussySally]

You can tell how much effort he put in the video ❤ The mic threw me off but really nice video, man!

[pre-universitygeometricalg]

Very useful. Thanks. I'll add it to playlists on our channel.

[swag_designs]

This was amazing I loved it thank you❤

[spiderjerusalem]

what abstract algebra did u use to learn from?

[pochotom]

Why is it not taught this way in engineering universities?

[BongoFerno]

How do you use nilpotent versors ε²=0 to get the velocity and acceleration for free?

[hotbit]

"Let i = e1e2" ... WHY? What I'm looking for is understanding, instead, usually people juggle words (like i, e1 etc.) according to some syntax rules and that's it. Therefore, it's some playing within linguist8ics system.
Also, in 10 min. video, talking fast, people pack a tonne of information, as if they (and viewers) are so smart. But I don't see this cleverness in the real world. That's why I don't like your video.