filmov
tv
8.2 Circular Motion: Position and Velocity Vectors

Показать описание
MIT 8.01 Classical Mechanics, Fall 2016
Instructor: Dr. Peter Dourmashkin
License: Creative Commons BY-NC-SA
Instructor: Dr. Peter Dourmashkin
License: Creative Commons BY-NC-SA
8.2 Circular Motion: Position and Velocity Vectors
Uniform Circular Motion Formulas and Equations - College Physics
Uniform Circular Motion and Centripetal Force
8 2 Uniform Circular Motion
Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration
Angular Motion and Torque
Uniform Circular Motion: Crash Course Physics #7
banked curves and circular motion explained
Electromagnetic Waves Ncert Solutions Class 12 | Full Chapter as per 2024-25 Syllabus
Derivation of Formula for Centripetal Acceleration v^2/r
Circular Vs Rotational Motion | #byjus #ytshorts #physics
Uniform Circular Motion
9.2 Uniform Circular Motion: Direction of the Acceleration
Angular Momentum Demo Arms IN vs OUT
Important formulas of #speed #Distance and #time #shorts
11.1 Newton's 2nd Law and Circular Motion
Rotational Motion: Crash Course Physics #11
Parvez Khan Sir | physics on top 😅| Circular Motion #parvezkhansir #unacademy #kota
JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts
Direction of velocity in Uniform Circular motion | DIY experiment | BYJU'S
Magnetic fields demonstration 🧲
👀 Asking GCSE Students (Hamdi) How Much They Physics They Know - Part 1 #Shorts
10.1 Circular Motion - Acceleration
How satellite moves around the earth .
Комментарии
 0:06:02
0:06:02
 0:12:43
0:12:43
 0:06:12
0:06:12
 0:32:06
0:32:06
 0:11:28
0:11:28
 0:07:39
0:07:39
 0:09:54
0:09:54
 0:05:36
0:05:36
 1:07:16
1:07:16
 0:03:59
0:03:59
 0:00:59
0:00:59
 0:09:14
0:09:14
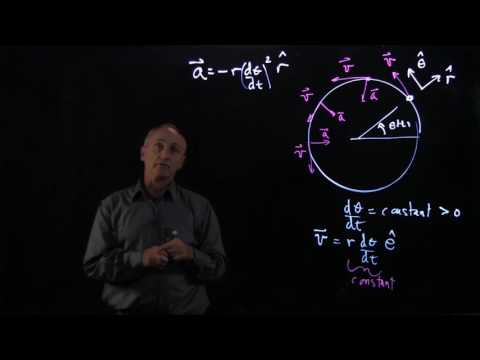 0:03:36
0:03:36
 0:00:47
0:00:47
 0:00:14
0:00:14
 0:03:17
0:03:17
 0:08:55
0:08:55
 0:00:20
0:00:20
 0:00:12
0:00:12
 0:01:00
0:01:00
 0:00:15
0:00:15
 0:00:37
0:00:37
 0:04:00
0:04:00
 0:00:14
0:00:14