Heat equation: How to solve

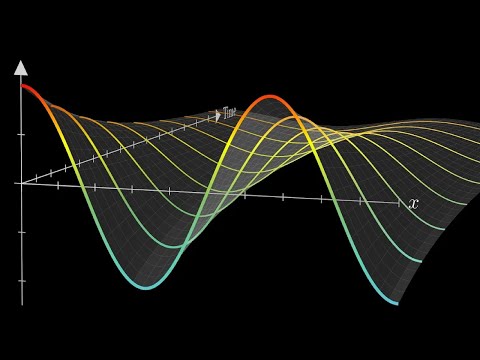
Suppose one has a function u that describes the temperature at a given location (x, y, z). This function will change over time as heat spreads throughout space. The heat equation is used to determine the change in the function u over time. The rate of change of u is proportional to the "curvature" of u. Thus, the sharper the corner, the faster it is rounded off. Over time, the tendency is for peaks to be eroded, and valleys filled in. If u is linear in space (or has a constant gradient) at a given point, then u has reached steady-state and is unchanging at this point.
One of the interesting properties of the heat equation is the maximum principle that says that the maximum value of u is either earlier in time than the region of concern or on the edge of the region of concern. This is essentially saying that temperature comes either from some source or from earlier in time because heat permeates but is not created from nothingness. This is a property of parabolic partial differential equations and is not difficult to prove mathematically (see below).
Another interesting property is that even if u has a discontinuity at an initial time t = t0, the temperature becomes smooth as soon as t greater than t0. For example, if a bar of metal has temperature 0 and another has temperature 100 and they are stuck together end to end, then very quickly the temperature at the point of connection will become 50 and the graph of the temperature will run smoothly from 0 to 100.
The heat equation is used in probability and describes random walks. It is also applied in financial mathematics for this reason.
It is also important in Riemannian geometry and thus topology: it was adapted by Richard Hamilton when he defined the Ricci flow that was later used by Grigori Perelman to solve the topological Poincaré conjecture.

[DrChrisTisdell]

Thank you for your comment. I wish you all the best with your studies.

[paulestrada]

You are a life saver. I have a midterm coming up and did not want to just memorize this solution. I now have a much better understanding of how to derive a solution for the heat equation. Everything clicked for me after I saw this video and many others that you have posted regarding the wave equation as well.

[yoshuahutagalung]

Hi, thank you so much for the video. But can you give us the sequences of the video? I mean the order of which video we should watch first. Once again, thank you!

[johnadams]

mr.tisdell sir you are a boss :D, i don't even go my maths lecturer class and i ace all my course work because you your vids and you teach way better than him, a few people from our class in chemical and mechanical engineering in the Caribbean respect your teaching skills keep it up

[akzakirp]

Hello Dr Tisdell! I want to thank you about the wonderful lecture. It helped me alot! I just have 2 more questions:

1. How do we take the derivative at 17:40min dQ/dx? Can you please give me a hint about that?
2. and I have the initial concentration phi(y)=erfc(x^2/4kt) and the programs that I am using (maxima and mathematica) just can't solve that. Why is that?

Thanks again for making complicating problems so manageable!

[MerrillHutchison]

At 15:45, what allows you to switch from Qx(x-y, t) to -Qy(x-y, t) in the integrand in the next to last line? Also, which substitutions do you use for the integration by parts?

[AldoIanni]

At 16:00 why the derivative Qy(x-y) goes away in the u(x, 0) integral equation?

[SAMAmUrl]

This presentation was awesome, thanks a lot for this step by step and accurate work.. 

[huisun]

There is a slight mistake when you are applying the dilation property of the solution to heat equation to prove $Q(x, t)=g(s/\sqrt(4\pi t))$. That is, $a$ needs to be a constant, but you use $a=1/(4/\pi t)$. However, I'm aware that this is a standard mistake people make in textbooks and does not affect the conclusions at all. 

[Nebulae]

Thank you very much. This video has been very useful. And clarified a couple of things.

[adityakapoor]

In the slide at 9:09, the first g' is the partial diff of g( ) wrt t, while the second g' is the partial diff of g( ) wrt x. How can you just treat them as the same and add them then? Your clarification would be of great help!

[maemarkowski]

At 17:00, could you please explain how the integral from -infinity to x of Q gives you 1 when I thought it was the other way around(based on the definition of Q)? It's still unclear to me how you split up that integral. 

Thanks for the videos!

[yarooborkowski]

Could we also solve the heat equation by method of characteristics like You did with other PDEs?
I mean that some function u=f(mx+t) can be solution to the heat equation. Then m has to satisfy f''*k*m^2 - f' = 0
And f has to be of A*e^(r*(mx+t)) form.
Do I go in right way to the solution?

[jeremiadumpling]

I think I’m a little confused as how to apply the heat equation in real problems. My question is what do you do with the solution when you have it? How do you actually find the temperature at point x at time t? Thanks!

[nazishahmad]

Which app u are actually using to create this type of content please tell

[suumrethwala]

HI,
what is the reason behind changing the initial condition from U(x, 0) = H(x) to
Q(x, 0) = 1, x>0 and Q(x, 0) = 0, x<0.
Thanks

[الهاشمي-شح]

hi Doctor I want you to help me ..How to solve the parabolic partial differential equation with by the presence of initial conditions and boundary conditions by separation of variables

[haraldtasti]

At 10:2 the solution to the ODE is written as z(p)=Ae^(-p^2). The correct solution is, however, as I can find different, namely Ae^(-2p). How do you get p raised to second power, when the correct answer is 2p?

[anshful]

hello sir... thanks for your solution. but i am not able to understand the last page of your given solution how to compute partial derivative of Q with respect to x, I am not able to solve it. plz help me...

[anshful]

Sir plz give me reply.. if anyone find this then please give me the answer