filmov
tv
Trig substitution integral x^3*sqrt(4-x^2) + triangle to evaluate cosine of inverse sine at the end.
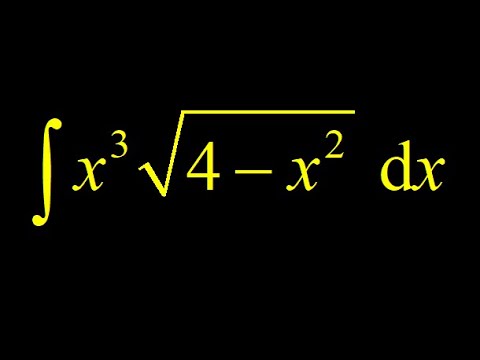
Показать описание
Questions or requests? Post your comments below, and I will respond within 24 hours.
Trig substitution integral x^3*sqrt(4-x^2) + triangle to evaluate cosine of inverse sine at the end.
When we see a square root in the integral with a variable piece squared inside, we immediately think to do a trig substitution!
In this trig sub integral, we start by making the substitution let x=2sin(theta). The motivation here is to simplify the interior of the square root using the trig identity (cos(x))^2=1-(sin(x))^2. We transform the integral in terms of theta.
Now we have a trigonometric integral (sin(x))^3*(cos(x))^2, and we get a handle on this trig integral by splitting off a factor of (sin(x))^2 and using the same pythagorean identity (sin(x))^2=1-(cos(x))^2.
This results in two integrals, each consisting of a power of cosine with a sine next to it. We can guess the antiderivatives using the chain rule backwards, and we arrive at the total antiderivative in terms of theta.
Finally, we have to transform the antiderivative in terms of x, but this requires evaluating the cosine of an inverse sine. We draw a triangle to evaluate cos(arcsin(x/2)) and express the final antiderivative in terms of simple algebraic functions of x.
Trig substitution integral x^3*sqrt(4-x^2) + triangle to evaluate cosine of inverse sine at the end.
Integral of x^3/sqrt(x^2+4) (substitution)
Trigonometric Substitution
Integration Example: Trigonometric Substitution #1
Calculus 2: Integration - Trig Substitution (6 of 28) Integral of x^3/SQRT(a^2-x^2) Ex.4
Integral (x^3)/(4x^2+9)^(3/2) dx
Calculus 2 Lecture 7.3: Integrals By Trigonometric Substitution
integral of sqrt(x^2-9)/x^3 by trig substitution, calculus 2 tutorial
Evaluate the integral using the indicated trigonometric substitution. (x^3)/sqrt((x^2)+9)
when calculus students use trig identities too early
Integration By Trigonometric Substitution
integral of sqrt(x^2-3)/x, trig substitution
integral x^3 sqrt(9-x^2) dx
Integrate sqrt(16x^2 + 25)/x^4 using Trigonometric Substitution
BONUS: IMPRESS YOUR CALC 2 TEACHERS
Trig sub completing the square: complete square before substitution. Integrate 1/sqrt(x^2+4x-12).
Integral 45: int x^3 sqrt{4-x^2} dx
Integral of sqrt(4-x^2) - Trigonometric Substitution.
Integral of sqrt(64 - 4x^2) using Trigonometric Substitution
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Calculus 2: Integration - Trig Substitution (3 of 28) Integral of SQRT(x^2-x^2) Ex. 1
Integration of Rational Functions By Completing The Square - Calculus
Trig substitution integration: x=a*tanθ, calculus 2
Integral of 1/(49 - x^2)^(3/2) using Trigonometric Substitution
Комментарии
 0:03:34
0:03:34
 0:19:50
0:19:50
 0:03:37
0:03:37
 0:07:49
0:07:49
 0:09:34
0:09:34
 2:09:24
2:09:24
 0:09:20
0:09:20
 0:07:06
0:07:06
 0:00:43
0:00:43
 0:15:55
0:15:55
 0:04:09
0:04:09
 0:12:15
0:12:15
 0:08:36
0:08:36
 0:06:55
0:06:55
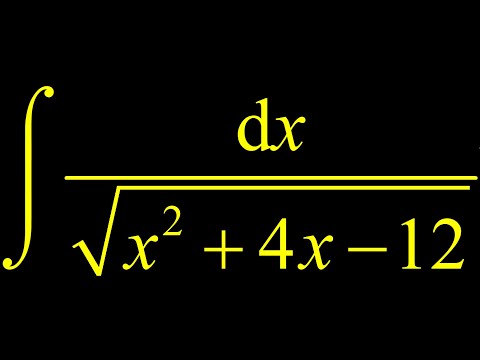 0:09:57
0:09:57
 0:07:19
0:07:19
 0:04:38
0:04:38
 0:06:27
0:06:27
 0:22:40
0:22:40
 0:08:52
0:08:52
 0:26:06
0:26:06
 0:20:50
0:20:50
 0:04:31
0:04:31