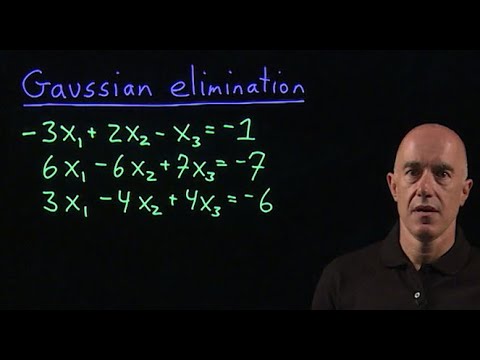Gaussian Elimination

I thought this was a cool visualization to show you guys.

Examples of Gaussian Elimination:

INTERNSHIP INFO:
Unfortunately, the deadline has passed. I'll let you guys know about future opportunities, though!

[filipsperl]

At first I thought this was 3blue1brown video, but then I've noticed it's only 5 minutes :)

[Alejandro-ruun]

I'm on my first semester of engineering and we just learned gaussian elimination. This visual representation has opened my eyes to what I'm really doing when applying the algorithm. thanks a, lot great content!

[solhe]

OMG im a math major and it's final week and im losing interests in math (cuz of the stress), this got me interested in it again! thank you!

[thesuki]

Wow I wish I saw that visualization while I took linear algebra as an undergrad. It makes a lot of sense geometrically.
2:00 “sorry for the messy chalkboard” ha! I wish my chalkboard was that organized when I TA.

[patrickl]

Wish this guy still made content. Feel likes he's the kinda guy who would steadily improve his content, if he was able to be consistent. Might become something special

[juniorcyans]

The visualization really helped me to understand the concept! Thanks a lot!

[Madsy]

Nice work, LeiosOS. Especially the visual explanation :-)

[alwysrite]

beautiful stuff ! thanks for the visual representation which is never taught in schools

[joshuaronisjr]

Amazing video! Thank you, for this and all your videos!


I just want to provide a quick explanation about something that confused me when I was learning this. It's mostly for me if I watch this in the future, but maybe it helps someone else!!


Starting at 3:10


"Each row in our matrix is itself an equation for a plane"


That is, the (x, y, z) solution to each row of our equation gives us all (x, y, z) vectors whose endpoints lie on a plane.


To elaborate, all vectors whose dot product with [2, 3, 4] is equal to 6 have endpoints on the blue plane. All the vectors whose dot product with [1, 2, 3] is 4 have endpoints on the red plane. And all vectors whose dot product with [3, -4, 0] is equal to 10 have endpoints on the green plane.


"Their points of intersection is the solution we found before"


The intersection of the three planes is the endpoint of a vector whose dot product with the first row of our matrix is 6, whose dot product with the second row of the matrix is 4, and whose dot product with the third row of the matrix is 10. It satisfies all three requirements of our matrix equation, so it's the solution to the equation.


"No matter how we change the planes with Gaussian Elimination, the solution remains the same."


Let r1 denote the first row vector of our matrix, r2 the second row, and r2 the third row.


Let x denote the solution.

r1 dot x = 6
r2 dot x = 4
r3 dot x = 10


Now, what's a dot product? What's the geometric interpretation of r1 dot x?


r1 dot x the component of r1 that lies on x scaled by the magnitude of x.
r2 dot x is the component of r2 that lies on x scaled by the magnitude of x.


So, (r1+r2) dot x is the component of (r1+r2) that lies on x scaled by the magnitude of x.


From that interpretation, it becomes pretty geometrically obvious that if r1 dot x = 6, and r2 dot x = 4, then (r1 + r2) dot x = 10


Therefore, the vector x that satisfies (r1+r2) dot x = 6+4, or any other linear combination of the rows, must be the same vector that satisfied the original system of equations.


"The planes wobble about until one of them is parallel to 2 of the 3 axes"


Going back to the dot product picture, we're linearly combining the row vectors of our matrix until one of them lies entirely on one of the axes - in this case, where we're ending up with an upper triangular matrix, on the z axis.


Once a vector (r3) lies entirely on the z axis, its easy to solve for the z compnent of x that satisfies the new dot product equation.

[suzukigsxfa]

This is very helpful to see elimination visually. Very cool and elimination makes more sense now

[Omnifarious]

I've never seen that visualization before, and it was quite nifty.

[dafdaf]

You are doing an amazing job explaining hard topics intuitively. You need a hit video. I know it is hard but a video solely based on animations with an interesting topic, that might be presented to the general audience can give your hit. Good luck and keep up the good work!

[bhoomikasaxena]

Thanks...Now I understood what's the concept behind solving equations through matrices

[VincentZalzal]

It's very nice to see different visualizations for the same thing. You showed gaussian elimination by looking at the matrix row-by-row, where each row yields a plane equation. But you can also look at it column-by-column, where each column is the vector of the basis of that matrix. For those interested, keep reading :)

In effect, the matrix is a transformation function that can be applied to a point, and we know only the answer of applying it to a point. We want to know what point the transformation was applied to. In other words, we want to do the inverse transformation to the given point.

Applying the matrix to the usual (i, j, k) orthonormal basis yields a warped basis: i is mapped to the first column of the matrix, j to the second and k to the third. Gassian elimination operations can be seen as shearing and scaling transformations applied to both the warped basis and the point. After applying all the operations, the warped basis is back to the original (i, j, k) basis, and the point has been transformed to the answer we are looking for.

[PrettyMuchPhysics]

That's a very pretty visualization :D

[roshinroy]

Amazing explanation man.. I searched everything on YouTube for a clear explanation and finally found it in this video which I in fact skipped a couple of times…!!!

[Aperfull]

Thanks! Gaussian elimination always seemed to me like one of those math tricks that work but that no one takes the time to show why. This visualization made everything clear!!

[ManueGuitar]

WoW! Thanks for this video... I'm Electrical Engineer and now I understand the Gaussian Elimination for you! The 3D animation was amazing and very illustrative :D

[seasong]

I heard Gauss himself was able to solve this in third grade, which is absolutely crazy

[BryceDoesLife]

These are some of the best math videos on youtube.