Trigonometric Functions of Any Angle: Learn these Strategies

Alright, let's dive into the electrifying world of trigonometric functions, where every angle, no matter how quirky or ordinary, gets to show off its moves!

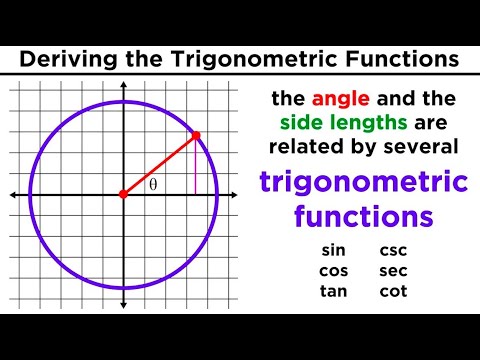
Picture trigonometry as the secret language of triangles, especially right-angled ones. Now, let's introduce the cool crew of trig functions, who are always up for a dance with any angle you throw at them, be it in a cozy corner of a circle or in the wild, wide angles beyond 360°.

1. Sine (sin) - Imagine you're at a concert, and the sound waves are bouncing off, creating that perfect vibe. The sine of an angle is like the height of those sound waves, reaching up or down from the center line. It's all about that vertical vibe, no matter where your angle is chilling on the circle.

2. Cosine (cos) - Now, picture sliding across the dance floor. Cosine keeps track of how far you've slid from the starting point, horizontally. Whether you're sliding left or right, cosine's got the moves to match every angle's horizontal groove.

3. Tangent (tan) - This one's the wild card. Imagine you're trying to climb a slippery slope. Tangent is that steepness or slope you're battling against. It can get really steep, really quick, especially when sine and cosine are in one of their dramatic showdowns.

But wait, there's more! Each of these functions has a sidekick, doing the reverse moves:

4. Cosecant (csc) - This is sine's inverse hype-man, focusing on the reciprocal of those vertical vibes.

5. Secant (sec) - Cosine's backup dancer, dealing with the reciprocal of the horizontal slides.

6. Cotangent (cot) - Tangent's mirror image, flipping the script to focus on the reciprocal of the slope.

Now, here's the kicker: these functions aren't just limited to angles in a cozy 0° to 90° range. They're globe-trotters, exploring angles in any direction, any size, even those that loop around the circle multiple times. Whether your angle is in degrees or radians, positive or negative, these trig functions are ready to translate it into the language of triangles and circles.

So, next time you're staring at an angle, whether it's lounging in a circle or skyrocketing into the trigonometric stratosphere, remember: the trigonometric functions are your translators, turning those angles into moves that can shake up the world of mathematics and beyond!