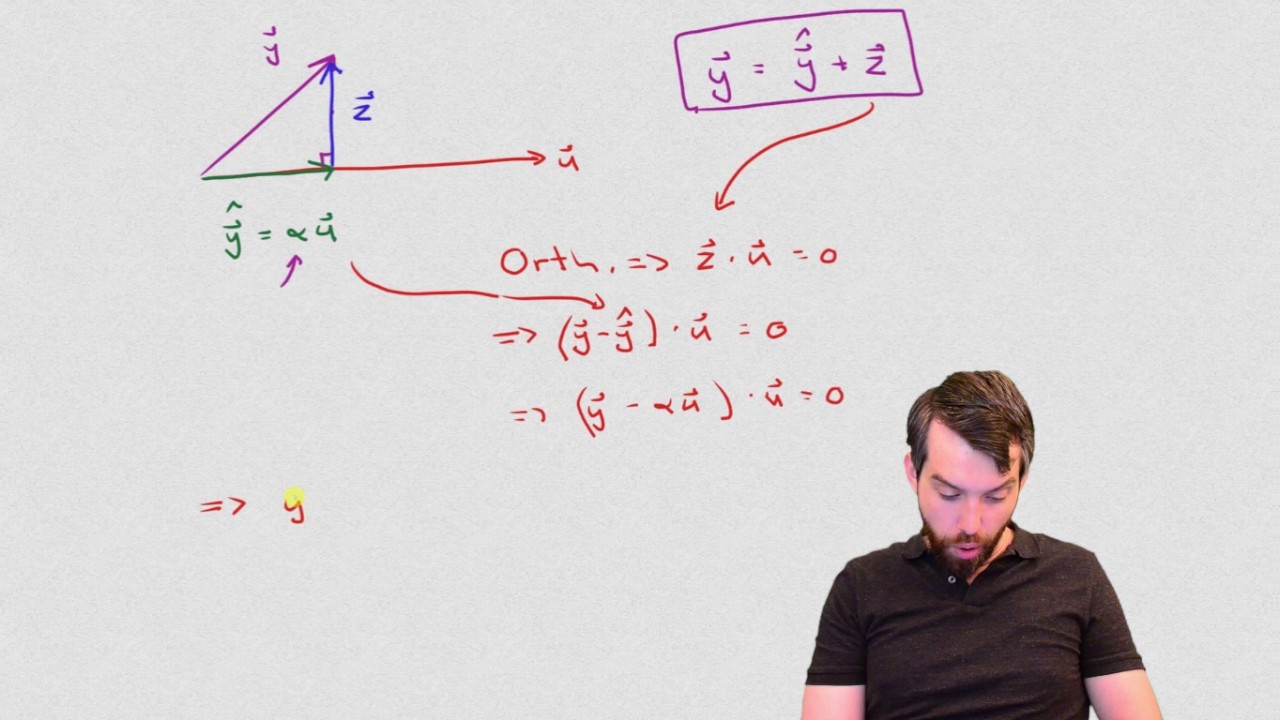
The geometric view on orthogonal projections

Learning Objectives:
1) Given a vector, compute the orthogonal projection onto another vector

This video is part of a Linear Algebra course taught by Dr. Trefor Bazett at the University of Cincinnati

[vocal.unrest]

This blew my mind and explained it way better than the textbook. Thank you!

[z.m.]

Thank you for the clear explanation, you are the best "textbook companion" ❤

[duncanweakley]

Love your enthusiasm as you explain, thanks for your content :)

[anthonyalvarez]

Best explanation seen so far. Actually the goat

[lukewood]

Explained better than I've seen it elsewhere. I'd be interested to see you explain it in terms of inner product spaces as well. thanks for the great video

[SalehGoodarzian]

Thank you very much. Such a great video, very helpful and educational. Best wishes to you

[mostafaahmadi]

Just beautiful and elegant. Incredible explanation. Thank you so much.

[hyperduality]

Affine projective geometry is dual to hyperbolic projective geometry.
Infinite (affine, canonical or standard) is dual to finite (hyperbolic or non standard).
Duality creates reality!

[beetlesstrengthandpower]

At the end x2 and x3 are given as vectors in the formula, but they are scalars right?

[manishajain]

Hello Sir, I have one doubt why do we want that y = y^ + z? Is it coming from Pythagoras theorem, but that has to be square if we are using Pythagoras theorem? Am I missing some result that you are using here?

[mortezakhoshbin]

Thanks alot.are the unit vector of spherical or cylendrical coordinates orthognal?

[Justkiddingbutuknow]

I've a question can u plz emplain to me why do we need to study orthogonal projection I mean what can we do with it??

[Darisiabgal]

You always get such glowing compliments but I finally had to give up on your series.
1. Sometimes you talk incredibly fast, and you run your syllables together, i have to go back and rerun some sections 2 or three times over.
2. You cannot see skyblue markers on a white back ground.
3. You write so small that even on an IPAD a alpha looks like a plus, you hats look like your vector marks and in some cases the characters are so small I have to blow up the image.
What that means if I am wasting alot of time trying to figure out what you are writing I'm not really understanding what you are saying particularly when you are rambling off stuff 100 MPH.