filmov
tv
These are orthogonal #shorts
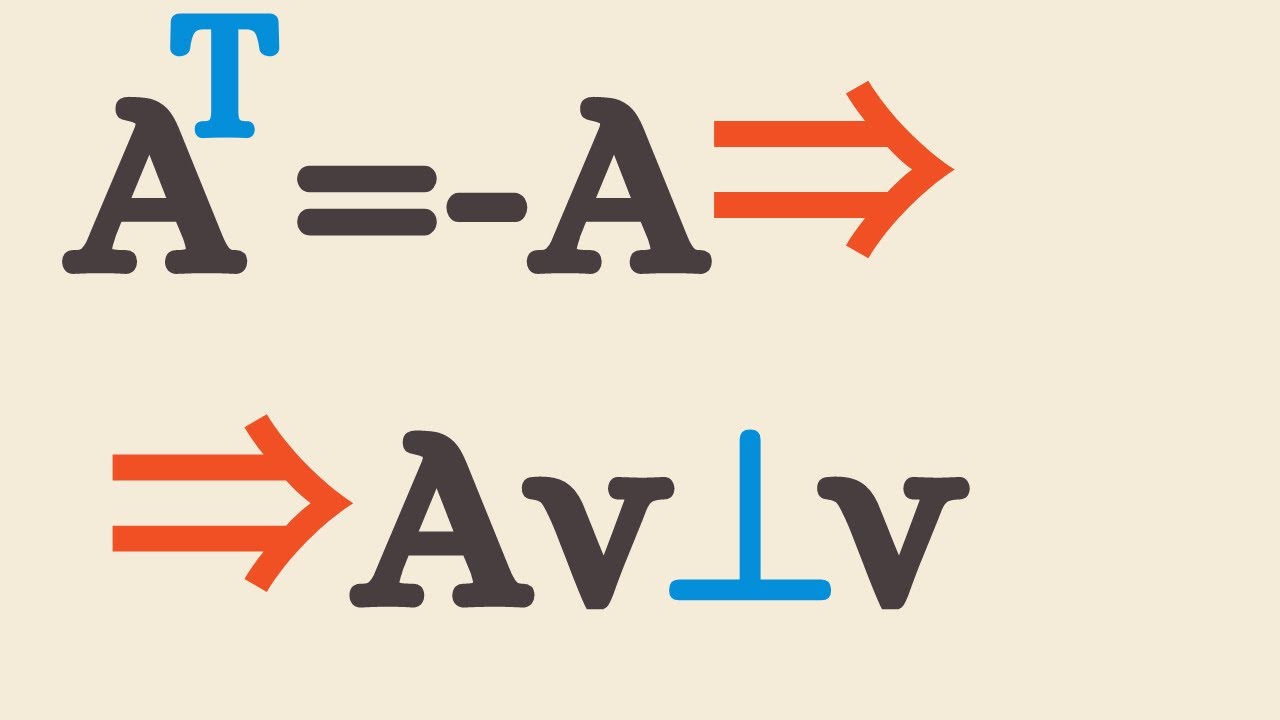
Показать описание
A better attempt at the format. #shorts
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
These are orthogonal #shorts
What is orthogonal?
Orthogonal
Game Terms Explained - Orthogonal #shorts
The Expert (Short Comedy Sketch)
Which is larger? #shorts
Difference Among Perpendicular, Normal and Orthogonal
If you think about (simplified for convenience) mathematical usage of 'orthogonal', it i.....
Physics Angular momentum operator 14 10 24 #Shorts #YouTube #Trending #Viral #News #Headlines
The Expert: Progress Meeting (Short Comedy Sketch)
Fusion:orthogonal✨ 🔛:Balance& Relaxation,↕️: Balance & strength #lehangacroptops #shorts #tr...
If you think about (simplified for convenience) mathematical usage of 'orthogonal', it i.....
orthogonal matrix | #short
Orthogonal Trajectory 2 - #Draw_with_MATH
What are orthogonal vectors/class 12 maths /vectors
Orthogonal Circles | Conic Sections #jeedailyconcepts #circles
Inverse of a Matrix
Orthogonal Trajectories Made Easy: Plotting in 1 Minute! #OrthogonalTrajectories #MathShorts
orthogonal cutting or oblique cutting 🤔 | Amazing technology | mechanical engineer
Position & Orthogonal Vectors #youtubeshorts #geometry #maths #mathstricks #physics #unit
orthogonal cutting using Abaqus
Orthogonal: an animated short by Ollie Rankin (2021)
difference between orthogonal and oblique cutting? in just 1 minute #metal cutting #manufacturing
Atlas Orthogonal chiropractic low force demonstration #lowforceadjusting #uppercervical
Комментарии
 0:00:58
0:00:58
 0:00:34
0:00:34
 0:00:12
0:00:12
 0:00:47
0:00:47
 0:07:35
0:07:35
 0:00:51
0:00:51
 0:00:43
0:00:43
 0:00:49
0:00:49
 0:22:45
0:22:45
 0:02:54
0:02:54
 0:00:20
0:00:20
 0:00:49
0:00:49
 0:00:59
0:00:59
 0:00:21
0:00:21
 0:00:13
0:00:13
 0:00:55
0:00:55
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:00:10
0:00:10
 0:00:19
0:00:19
 0:00:15
0:00:15
 0:03:49
0:03:49
 0:00:59
0:00:59
 0:01:01
0:01:01