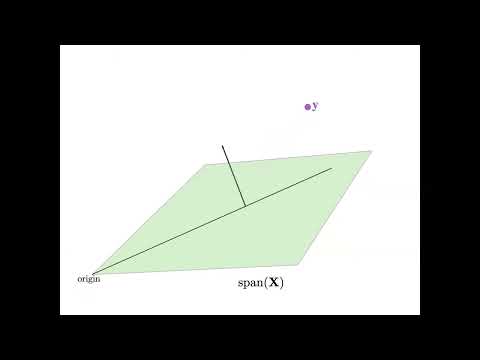
9 Regression as an Orthogonal Projection

preview_player
Показать описание

  1. Shaina Race Bennett
Рекомендации по теме
9 Regression 0:08:36

9 Regression as an Orthogonal Projection

9 Regression 0:08:36

9 Regression as an Orthogonal Projection

Orthogonal Regression 0:07:48

Orthogonal Regression

9.6) Orthogonal Partitioned 0:02:46

9.6) Orthogonal Partitioned Regression

Orthogonal regressors and 0:04:01

Orthogonal regressors and predictors

Multivariate Regression - 0:10:29

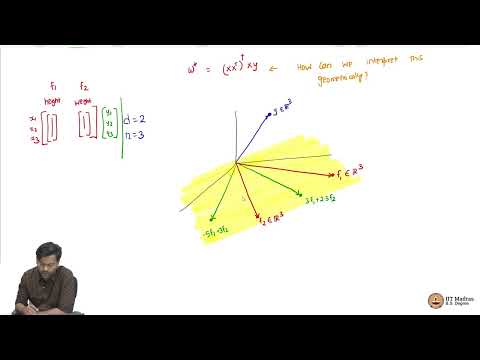
Multivariate Regression - Appendix - Orthogonal Projection

On orthogonal designs 0:07:36

On orthogonal designs and regression

BEST DEFENCE ACADEMY 0:00:15

BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb

Dot products and 0:14:12

Dot products and duality | Chapter 9, Essence of linear algebra

How much does 0:00:44

How much does a PHYSICS RESEARCHER make?

Psych Stats II: 0:49:44

Psych Stats II: Multiple orthogonal linear regression

Trying transition video 0:00:15

Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...

Projection into Subspaces 0:09:51

Projection into Subspaces

9.4) Orthogonal Projection 0:03:00

9.4) Orthogonal Projection Matrix

Multiple Regression Part 0:09:07

Multiple Regression Part 2 Orthogonal Coding

Aspirants Must Know 0:00:20

Aspirants Must Know The Value Of 1 minute #motivation #iitstatus #upscstatus #neetstatus #toppers

Most💯 Important Step 0:00:16

Most💯 Important Step Before any Procedure 🔥

9. Four Ways 0:49:51

9. Four Ways to Solve Least Squares Problems

Lecture31 (Data2Decision) Total 0:22:18

Lecture31 (Data2Decision) Total Regression, part 2

Period on the 0:00:41

Period on the road 😱 | Omg..

1st yr. Vs 0:00:20

1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet

Geometric interpretation of 0:13:17

Geometric interpretation of linear regression

Linear Regression and 0:06:36

Linear Regression and Robustness | Full course | Orthogonal Inputs

11 years later 0:00:11

11 years later ❤️ @shrads

Комментарии
Автор

That's amazing video, Beautiful explanation of linear regression in terms of linear algebra.

AlphansoEric
Автор

Great content! This was the missing link between my linear algebra and econometrics courses :D

MrOndra
Автор

This is just way too good. Thanks a lot!

breathemath
Автор

Thank you so much, you made algebra and linear regression click for me

antonlinares
Автор

I'm not sure this is what I am looking for, if it is, then I missed it. I have an implicit function f(x, y, z)=0 (it is actually a model with adjustable parameters). I have an experimental data point (Xexp, Yexp, Zexp). You can probably see where I am heading with this. I want to know where a line, orthogonal/perpendicular to the surface, will intersect the surface. I'm calling this point of intersection Xcalc, Ycalc, Zcalc. How do I proceed?

Based on other videos I watched, it looks like the first step is to linearize the surface using Taylor series. So, now I have a plane (in terms of partial derivatives and (Xcalc, Ycalc, Zcalc) which is still unknown. I want to know the point of intersection (Xcalc, Ycalc, Zcalc) of the orthogonal line from Xexp, Yexp, Zexp.

At first, I thought is it a trial an error iterative procedure (I have to guess Xcalc, Ycalc, Zcalc) so I programmed that, but the answers I am getting do not seem to be correct. I'm also beginning to suspect that the solution can be direct, not iterative.

Any thoughts?

sumsw
Автор

Very amazing lecture! thank you very much for your efforts. Is the line from the origin to the point y_hat the regression line please?

teklehaimanotaman
Автор

why do we begin at y sub zero and not y sub 1?

GregorianWater