filmov
tv
Is the sum of two periodic functions still periodic?

Показать описание
We know sin(x) is periodic and sin(πx) is also periodic. How about the sin(x)+sin(πx)?
Note: The "least common multiple" method helps to find "a" period of the sum but it does not guarantee that it is the shortest period.
10% off with the code "TEESPRINGWELCOME10"
blackpenredpen
Note: The "least common multiple" method helps to find "a" period of the sum but it does not guarantee that it is the shortest period.
10% off with the code "TEESPRINGWELCOME10"
blackpenredpen
What is the sum of 3/4 and 2/3?
Sum of Two Integers - Leetcode 371 - Java
Two Sum - Leetcode 1 - HashMap - Python
Is the sum of two periodic functions still periodic?
Sum and Difference
TWO SUM II - Amazon Coding Interview Question - Leetcode 167 - Python
2 Sum Problem | 2 types of the same problem for Interviews | Brute-Better-Optimal
Sum of 2 Squares Factoring
Big Tech Won't STOP Asking This Coding Interview Question | Two Sum
What is the sum of any two (a) Odd numbers(b) Even numbers.Ex 3.2-Playing with numbers -NCERT
Lil Baby - Sum 2 Prove (Lyrics)
Number Theory: The sum of two Odd numbers are Even
LeetCode Exercise in Java Tutorial - Two Sum FAST Solution
Draw a flowchart to find the sum of two numbers
the ratio of two numbers is 3:4 and their sum are 560. #shorts #maths #trending #viralshorts
L12.2 The Sum of Independent Discrete Random Variables
Sum of natural numbers 1 to 100
Python Programming Practice: LeetCode #1 -- Two Sum
The sum of two numbers is 11 and their difference is 5. Find the numbers // chapter 2 -class 8 // l
1. Two Sum - Leetcode (Python)
Factoring Sum and Difference of Cubes
The sum of two numbers is 18. If one is twice the other, find the numbers.Class 8- linear equation
Sum and Difference of Two Terms
Number Theory: The sum of two Even numbers are Even
Комментарии
 0:03:05
0:03:05
 0:11:48
0:11:48
 0:08:26
0:08:26
 0:07:36
0:07:36
 0:01:36
0:01:36
 0:08:18
0:08:18
 0:18:20
0:18:20
 0:02:25
0:02:25
 0:00:45
0:00:45
 0:02:05
0:02:05
 0:03:26
0:03:26
 0:04:22
0:04:22
 0:23:36
0:23:36
 0:00:58
0:00:58
 0:00:35
0:00:35
 0:07:52
0:07:52
 0:02:26
0:02:26
 0:13:09
0:13:09
 0:02:58
0:02:58
 0:03:30
0:03:30
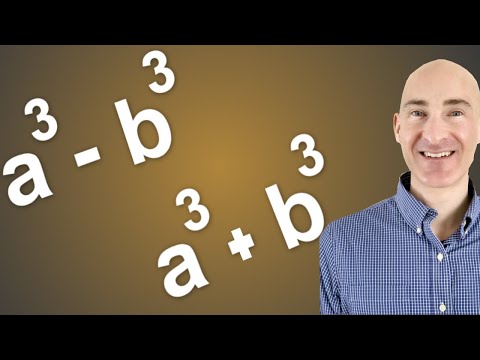 0:05:35
0:05:35
 0:02:52
0:02:52
 0:01:07
0:01:07
 0:05:17
0:05:17