filmov
tv
Prove the limit of 1/sqrt(3x+7) = 1/5 as x approaches 6 (using epsilon-delta) (ILIEKMATHPHYSICS)

Показать описание
This video references the book "Introduction to Real Analysis" by Bartle and Sherbert (Fourth Edition). For more details related to the types of exercises covered in this video, see section 4.1.
Thanks and enjoy the video!
Thanks and enjoy the video!
Prove the limit of 1/sqrt(3x+7) = 1/5 as x approaches 6 (using epsilon-delta) (ILIEKMATHPHYSICS)
Proof of a Limit Value Using Epsilon and Delta
how to easily write the epsilon-delta proofs for limits
Epsilon delta limit (Example 7): 1/x
This is a very famous limit
Epsilon delta limit (Example 6): Square Roots
Learn how to evaluate a limit at infinity
Examples on Epsilon Delta Definition of Limit (for 1 variable functions)
Calculus 1 Exam Review Part8
When mathematicians get bored (ep1)
How REAL Men Integrate Functions
How To Find The Limit At Infinity
limits with epsilon-delta definition! (linear, square root, and quadratic examples)
5 simple unsolvable equations
Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics
Limits of Trigonometric Functions
Evaluating Limits at Infinity of Rational Functions with Square Roots (Example)
Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon
AP Scores are out today
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Finding a Delta Given an Epsilon
Limits at Infinity & Horizontal Asymptotes
Functions IIT Questions NO 11 ( X Class)
Solving Limits Mentally #calculus #limit #infinity #rational
Комментарии
 0:08:34
0:08:34
 0:09:17
0:09:17
 0:08:28
0:08:28
 0:09:55
0:09:55
 0:00:48
0:00:48
 0:04:03
0:04:03
 0:01:40
0:01:40
 0:16:35
0:16:35
 3:10:17
3:10:17
 0:00:37
0:00:37
 0:00:35
0:00:35
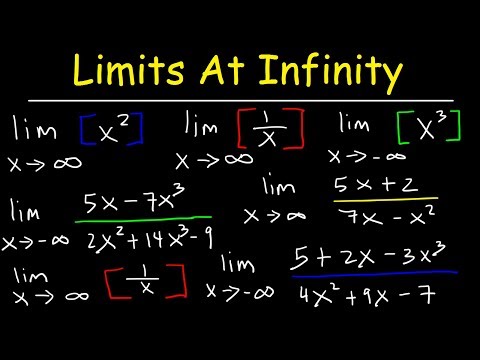 0:13:14
0:13:14
 0:15:21
0:15:21
 0:00:50
0:00:50
 0:00:11
0:00:11
 0:15:23
0:15:23
 0:04:53
0:04:53
 0:09:56
0:09:56
 0:00:51
0:00:51
 0:00:16
0:00:16
 0:13:41
0:13:41
 0:19:24
0:19:24
 0:00:48
0:00:48
 0:01:00
0:01:00