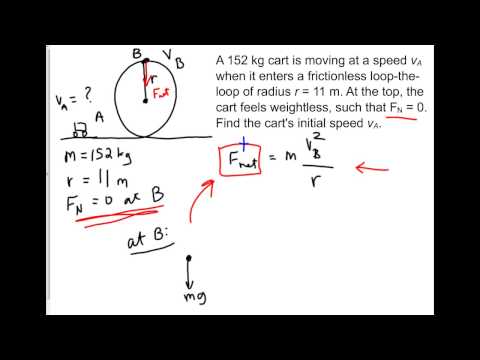
Loop-the-loop physics problem: Forces on a vertical loop.

I solve the loop the loop first year undergraduate and AP physics problems

[joshuarobbins]

Thank you so much! I'm currently in physics right now and it's probably the class i've struggled with the most lol

[PhysicsNinja]

Visit my site to download the PDF of the solution.

[kevinjmn]

Thanks so much. I am a freshman in college and was stuck on this homework problem for an hour.

[AzulaOTP]

I figured it out by myself after seeing "conservation of energy" in the beginning of the video. I did not think of using those laws, makes a lot of sense now!

[vijgenboom]

❤️ A BIG thank you! May the LORD bless you.

[Happy.Traveller]

Hello Physics Ninja, I have 2 questions:

1) Why does the gravitational potential energy at the top of the hill have to equal the total energy at the top of the loop? Shouldn't it be less, because at the top of the hill, there is the additional energy from kinetic energy? (m and g would be constant and since we don't know r, for all you know it could be equal to h.)

2) Someone's already asked this before but it wasn't answered properly. At 8:20, you said "we want the contact force to be equal to zero". Why though? When the contact force is equal to zero, the object falls off the track and that's exactly what we DON'T want. (Also you wrote "N does not equal to 0" so was this just bad wording?)

Related to this:
At 8:08 you said at some point the term in the left is equal to g. Why? Is it because at the very top of the loop, the only acceleration or energy is the downward acceleration is just due to gravity, or g?

Thank you.

[kornelviktor]

Great video, but I have a question: If h is equal to 2r then how to calculate the maximum height that the car can reach. In another words the height when the car will fall down

[Omer-ysys]

Thank you for your videos your getting me through college

[lionbearpolarbear]

Can you explain why we have v=sqrt(gR) ? Why do we want the contact force to be equal to zero? Doesn't that mean that the object going around the loop would fall off?

[maddieschwieters]

So, why does it NOT work to release the object from a position equal to the height of the top of the loop? Why must it be higher? 
Does the release location have to be higher because then it will provide the object enough speed to make it around the loop?
Thanks in advance!

[NK]

I really enjoy your physics vids! I’m a chemist (not a physicist..) and also a aviation. adventurist. There is a small group of us aviation adventurists working on an aviation loop FIRST attempt (the reason for being vague). I have started working on the physics behind our project but I’m not a physicist. Would you be will to discuss one on one our little physics problem?

[johnmifsud]

"tiny little " lovely tautology, keep it up...

[fubrian]

This expression only works when there is no friction on the track. If you are trying to make a real vertical loop, I recommend you make the height of your hill at least 3.5 times the radius of the loop.

[Geeky_Jake]

If there were a straight length/segment after the hill and before the loop that experienced friction and a friction coefficient, how could we determine the minimum height (of the hill) and speed (at the end of the segment)?

[heretocomment]

Hi @PhysicsNinja, you have proven that regardless of the radius of the loop and height of the hill, when relying only on gravity, the relationship is always the height is 2.5r. My question is, what is the distance between the base of the hill and the entry point of the loop? In other words, the moving object has to travel a certain horizontal distance on the ground once it reaches the bottom of the hill before it starts to incline and go up the loop - for h = 2.5r, what is this distance and how does this formula change if the distance is changed? Also: is there a limit to the length of the object? Imagine an amusement park ride - a train of several carriages and metres long would have a trail behind it as the first car enters the loop, would that not drag and slow it down and prevent it from entering the incline to complete the loop? Thanks.

[smulktis]

why is the "normal" force acting "down" in this case? wouldn't the object experience a normal force more similar to a "hugging the road" force that can be seen in a race car going around a steep incline turn?

[Ur_buddy_Pianomeastro]

If I have 2 marbles of different mass, your equation shows both should make the loop if I give them the height as per the formula. But thats not correct when I do the experiment

[alexsanderdumasig]

thank you so much but what if it has a gap after the loop?how can you solve it?

[marcosduronto]

thanks for the problem, i have aquiestion, i understand how to get the minimum velocity and that happen when normnal force in the top of the loop is 0, but also for the mass to fall from the loop the normalforce has to be 0, can you enlight me? sorryfor my englishiamfromargentina spanish is our natural language

[mmdarwani]

Thank you so much, This was very helpful