filmov
tv
How to find the first five terms of a geometric sequence
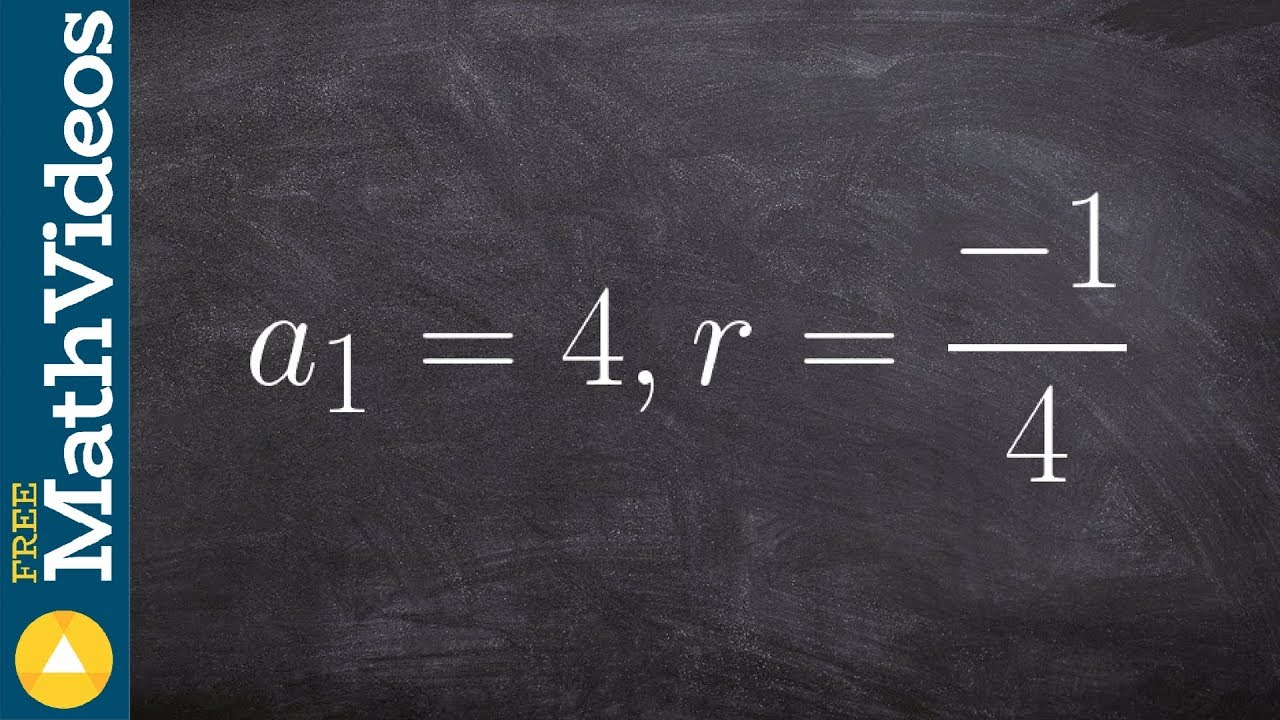
Показать описание
👉 Learn how to find the first 5 terms of a geometric sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. A geometric sequence is a sequence in which each term of the sequence is obtained by multiplying a pre-determined value, called the common ratio, to the preceding term.
The formula for the nth term of a geometric sequence is given by An = ar^(n - 1), where a is the first term, n is the term number and r is the common ratio. We can obtain the common ratio by dividing a term by the preceding term or if the known terms are not consecutive, we can obtain the common ratio by taking the nth root of the quotient of the two terms, where the n in the nth root is the difference of their term numbers. Plugging the required values into the formula, we can obtain the first five terms or the required terms of the geometric sequence.
Organized Videos:
✅ Sequences
✅Sequences | Learn About
✅Determine The First Five Terms of The Arithmetic Sequence
✅How to Write The Formula for a Arithmetic Sequence
✅Find the nth Term of an Arithmetic Sequence
✅Find the First Five Terms of a Geometric Sequence
✅How to Write The Formula for a Geometric Sequence
✅Find the nth Term of a Geometric Sequence
✅How to Determine Arithmetic or Geometric Sequence
✅Find the First Five Terms of a Sequence
✅How to Write The Formula for a Sequence
✅Find the nth Term of a Sequence
✅How to Simplify Factorials
✅Recursive Sequences
✅Prove the Sum by Induction
✅Find the Given Term of Binomial Expansion
✅Binomial Expansion | Learn About
✅How to Expand a Binomial
Connect with me:
#sequences #brianmclogan
The formula for the nth term of a geometric sequence is given by An = ar^(n - 1), where a is the first term, n is the term number and r is the common ratio. We can obtain the common ratio by dividing a term by the preceding term or if the known terms are not consecutive, we can obtain the common ratio by taking the nth root of the quotient of the two terms, where the n in the nth root is the difference of their term numbers. Plugging the required values into the formula, we can obtain the first five terms or the required terms of the geometric sequence.
Organized Videos:
✅ Sequences
✅Sequences | Learn About
✅Determine The First Five Terms of The Arithmetic Sequence
✅How to Write The Formula for a Arithmetic Sequence
✅Find the nth Term of an Arithmetic Sequence
✅Find the First Five Terms of a Geometric Sequence
✅How to Write The Formula for a Geometric Sequence
✅Find the nth Term of a Geometric Sequence
✅How to Determine Arithmetic or Geometric Sequence
✅Find the First Five Terms of a Sequence
✅How to Write The Formula for a Sequence
✅Find the nth Term of a Sequence
✅How to Simplify Factorials
✅Recursive Sequences
✅Prove the Sum by Induction
✅Find the Given Term of Binomial Expansion
✅Binomial Expansion | Learn About
✅How to Expand a Binomial
Connect with me:
#sequences #brianmclogan
0:10:37
Lec-5: Find First() in Compiler Design | First() & Follow() | Compiler Design
0:11:53
FIRST() and FOLLOW() Functions
0:09:27
Lec-6: Find FOLLOW() in Compiler Design | Learn First() & Follow() in Easiest way
0:02:46
How to find the first four terms of a sequence
0:12:34
How to find the FIRST THERMAL on your paraglider!
0:04:21
How To Find First Bug in Bug Bounty | Ethical Hacking
0:04:32
Find the first several terms of a sequence with given two terms
0:02:57
How to Find Your FIRST YouTube Subscriber!
0:13:26
Want to Sell on Amazon? Here’s How to Find Your First Winning Product!
0:05:31
THE FIRST DESCENDANT - HOW TO FIND AND UNLOCK ENCRYPTED VAULTS!
0:01:03
Where To Find The First Landmark From Arthur's Treasure Map In Hogwarts Legacy
0:08:18
All Fruit Locations in First Sea Blox Fruits. How to find Blox Fruits for Free in 1st Sea. Guide.
0:05:21
Arithmetic progression, find the. first term and common ratio.
0:05:12
Geometric Sequences: Find the first term and common ratio
0:07:49
How to Find Your First Wholesaling Deal in JUST 2 DAYS!
0:02:01
HOW TO FIND FIRST ADDRESS,LAST ADDRESS AND NO. OF NETWORK
0:20:06
How To Find Your First Amazon Online Arbitrage Product (BEST Beginner Method)
0:05:33
How to Find Good First Issues in Open Source?
0:02:07
How to find the first five terms of a geometric sequence
0:10:03
I PROMISE that you will find your first copywriting client
0:11:41
Find The Deal First or Find The Cash Buyer First?
0:04:25
How to find the first term and common ratio of a geometric series (two unknowns)
0:14:26
Find the common ratio and first term, 12th term and s of the first 10 terms.
0:20:34
Lecture 17 6 examples to find First and Follow | Most Important for exams
Комментарии