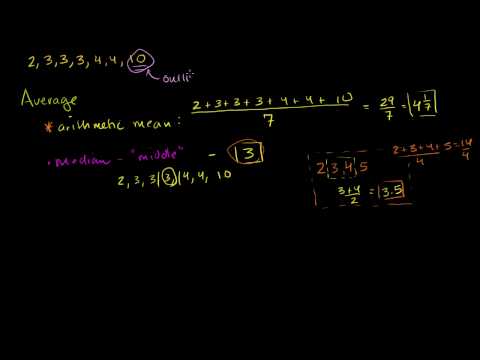Statistics | Measure of Central Tendency

Показать описание

Measures of Central Tendency

Introduction

A measure of central tendency is the use of a single value to describe a set of data by identifying the central position within that set of data. As such, measures of central tendency are sometimes called measures of central location. They are also classed as summary statistics. The mean (often called the average) is most likely the measure of central tendency that you are most familiar with, but there are others, such as the median and the mode.

The mean, median and mode are all valid measures of central tendency, but under different conditions, some measures of central tendency become more appropriate to use than others. In the following sections, we will look at the mean, mode and median, and learn how to calculate them and under what conditions they are most appropriate to be used.

#Mean (Arithmetic)

The mean (or average) is the most popular and well known measure of central tendency. It can be used with both discrete and continuous data, although its use is most often with continuous data (see our Types of Variable guide for data types). The mean is equal to the sum of all the values in the data set divided by the number of values in the data set. So, if we have n values in a data set and they have values x1,x2, …,xn, the sample mean, usually denoted by x¯ (pronounced "x bar"), is:
(x1+x2+ …+xn)/n

#Median

The median is the middle score for a set of data that has been arranged in order of magnitude. The median is less affected by outliers and skewed data. In order to calculate the median, suppose we have the data below:

65,55,89,56,35,14,56,55,87,45,92

We first need to rearrange that data into order of magnitude (smallest first):

14,35,45,55,55,56,56,65,87,89,92

Our median mark is the middle mark - in this case, 56. It is the middle mark because there are 5 scores before it and 5 scores after it. This works fine when you have an odd number of scores, but what happens when you have an even number of scores? What if you had only 10 scores? Well, you simply have to take the middle two scores and average the result. So, if we look at the example below:

65,55,89,56,35,14,56,55,87,45

We again rearrange that data into order of magnitude (smallest first):

14,35,45,55,55,56,56,65,87,89

Only now we have to take the 5th and 6th score in our data set and average them to get a median of 55.5.

#Mode

The mode is the most frequent score in our data set. On a histogram it represents the highest bar in a bar chart or histogram. You can, therefore, sometimes consider the mode as being the most popular option.