filmov
tv
Quadratic ceiling floor inequality
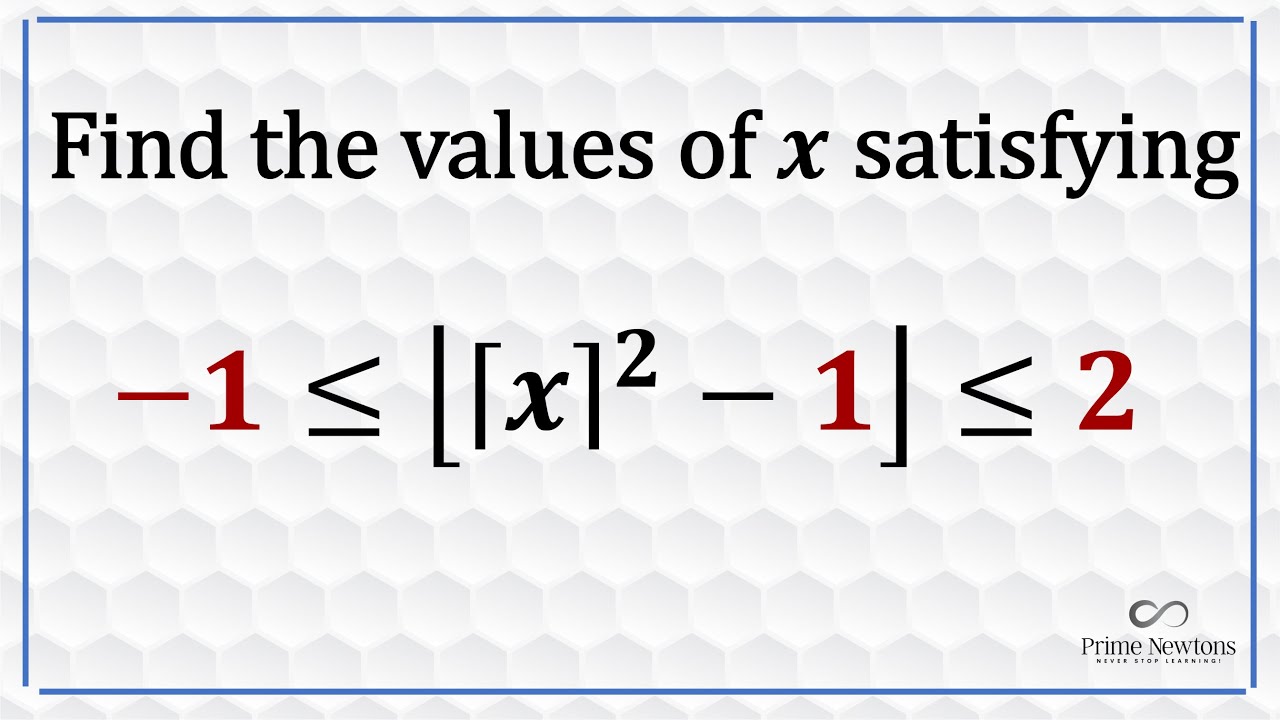
Показать описание
In this video, I soleved an inequality of the floor of a quadratic ceiling function. Yeah, it sounds confusing.
Quadratic ceiling floor inequality
Bounding Floor and Ceiling Function Sums
An equation with floor values! An algebraic adventure in equations and inequalities...
Quadratic Floor Equation
CMO 1999 | A quadratic floor function equation
A Quadratic Equation With the Floor Function | Canadian National Mathematical Olympiad 1999
Solving a Quadratic Floor Equation
A quadratic floor equation.
QUADRATIC EQUATIONS | Practice Questions | NDA MATHEMATICS
Similar To Quadratic Floor Equation
Floor and Ceiling Functions
Solving a Quadratic Floor Equation
Solving a Floor and Ceiling Equation
A floor value equation
Algebra: Equation with Floor and Ceiling
Solving A Floor Equation | Special Functions
A Nice Equation on the Floor Function | Baltic Way 1991
A Floor and Ceiling Equation, Floor(x-Ceil(x/2))=3
A ceiling and floor equation
A Floor and a Ceiling Equation ⌊x/2⌋=⌈x/3⌉
Algebra: Crazy Nested Floor Equation
functions explained in 17 seconds! (Algebra 1)
This 'Quadratic' Is Not Easy to Solve!
Solving Quadratic Inequalities PART II
Комментарии
 0:08:26
0:08:26
 0:08:47
0:08:47
 0:09:15
0:09:15
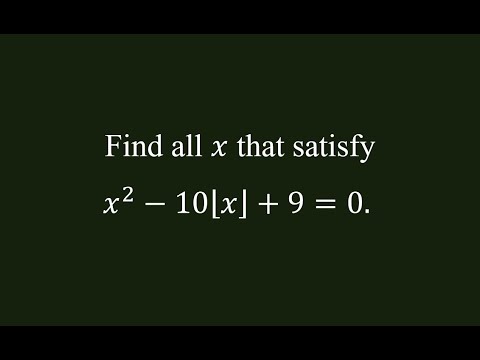 0:03:29
0:03:29
 0:09:32
0:09:32
 0:09:34
0:09:34
 0:13:28
0:13:28
 0:13:27
0:13:27
 1:50:58
1:50:58
 0:04:31
0:04:31
 0:05:09
0:05:09
 0:13:28
0:13:28
 0:06:07
0:06:07
 0:12:25
0:12:25
 0:04:39
0:04:39
 0:00:40
0:00:40
 0:08:42
0:08:42
 0:07:13
0:07:13
 0:08:26
0:08:26
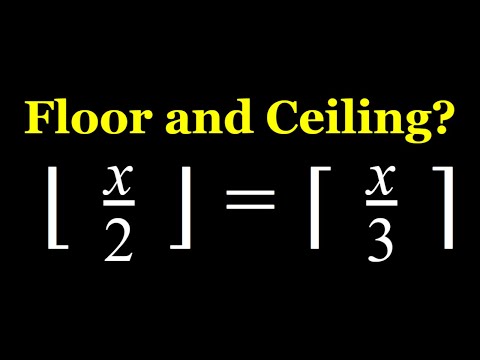 0:07:54
0:07:54
 0:13:54
0:13:54
 0:00:21
0:00:21
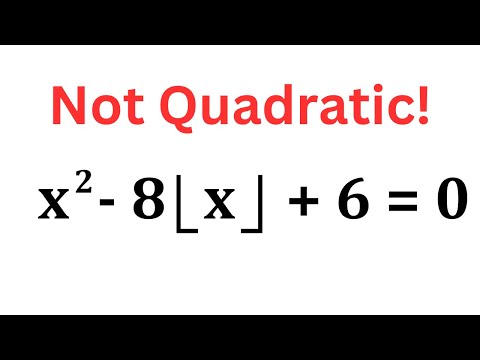 0:16:08
0:16:08
 0:07:02
0:07:02