Comparing {sqrt(2)}^{sqrt(7)} and {sqrt(3)}^{sqrt(3)}

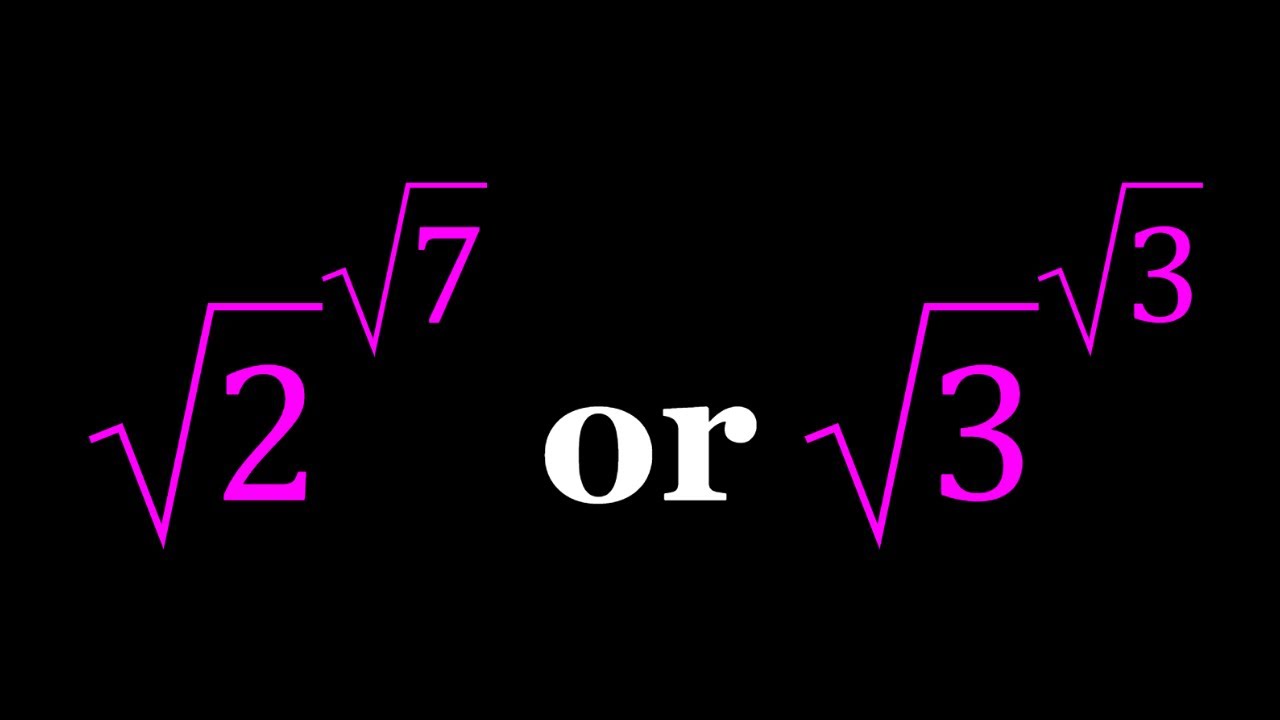
preview_player
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡

If you need to post a picture of your solution or idea:
#NumberTheoryProblems #ComparingNumbers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :

  1. SyberMath
Рекомендации по теме
Comparing {sqrt(2)}^{sqrt(7)} and 0:08:54

Comparing {sqrt(2)}^{sqrt(7)} and {sqrt(3)}^{sqrt(3)}

Comparing 2^sqrt(7) and 0:08:40

Comparing 2^sqrt(7) and 3^{13/8}

🔴Nice Square Root 0:00:55

🔴Nice Square Root Math Problem #maths

Do you remember 0:00:11

Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics

Human Calculator Solves 0:00:34

Human Calculator Solves World’s Longest Math Problem #shorts

Which is greater 0:02:49

Which is greater \( \sqrt{7}-\sqrt{3} \) or \( \sqrt{5}-1 \) ?

Square Roots in 0:01:00

Square Roots in No Time | Amazing Trick | #ytshorts #byjus #mathtricks #squareroot

Questions I get 0:00:16

Questions I get as a human calculator #shorts

Tetration ka ye 0:00:51

Tetration ka ye kaisa Question? 😱 #PW #Shorts #Maths

How to Compare 0:00:57

How to Compare Radicals with Different Radicands and Indexes #algebra #radicals

A Nice Olympiad 0:00:52

A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents

Largest & Smaller 0:00:37

Largest & Smaller Square Root Problem Solve #trick

How to compare 0:00:39

How to compare the 2 square root number | square root | surds. #shorts

How to Estimate 0:02:21

How to Estimate the Square Root of Non-Square Numbers

Speed Mental Math 0:00:14

Speed Mental Math Exercise #shorts

How To Do 0:00:42

How To Do comparison of 2/3, 3/5 and 3/7 // Maths In #Shorts// Incredible Gurukul

Magic trick to 0:00:12

Magic trick to find square roots ORALLY! #shorts #youtubeshorts #squareroots #baharlahamadhumas

Rules of Exponents 0:00:15

Rules of Exponents (Multiplying, Dividing, Roots) Algebra with JusticeTheTutor #math #shorts

Topper Vs Back 0:00:13

Topper Vs Back bencher | Exterior Angle Property #shorts #youtubeshorts #ashortaday #viralmaths #fun

Memorization Trick for 0:00:15

Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school

The Hardest Problem 0:00:31

The Hardest Problem on the SAT📚 | Algebra | Math

😳 CLEAN BASIC 0:00:05

😳 CLEAN BASIC MATHEMATICS 4/5+6/5+7/5=? #Shorts

Comparison | square 0:00:28

Comparison | square root | fraction | surds. #shorts #shortvideo

Trick! 0:00:22

Trick!

Комментарии
Автор

You did put the cart in front of the horse - means you knew the answer and stared from 2^14 against 3^9.
Normally you had to go other way. and come to 2^7 against 3^√21. Then logically you start bounding √21. The simplest guess is that √21>4.5 what is fortunately true. Then to get rid of 0.5 you square both sides/ Same what you did but in a natural way.

vladimirkaplun
Автор

i think you need to review the part from 2:30 to 2:50 !

abdeba
Автор

You can also directly calculate the numbers in excel and compare. The story is valid because it concerns positive numbers and squaring c.q. square rooting (being increasing functions then) does not change the order.

mystychief
Автор

I would guess {sqrt(k)}^{sqrt(k)} is always > {sqrt(k-l)}^{sqrt(k+l)} as long as k-l>0.

JXSJ
Автор

Elevo al quadrato.. 2^sqrt7 or 3^sqrt3.. Elevo a sqrt17, risulta 2^sqrt119 or 3^sqrt51..il primo numero è <2^11=2048..il secondo è >3^7=2187...

giuseppemalaguti
Автор

I can't say that my approach to solving this was valid, but I still guessed correctly!

scottleung
Автор

So thought_provoking...
Good job...👌👌👌.

mehrdadbasiri
Автор

SyberMath, I believe I've solved your problem in a much simpler way! Can I send you my solution?

syedmohammadhasanbintariqu
Автор

Jake multiple √3 by ln√3/ln√2 and see if it is greater than √7 and u are done

Chris_
visit shbcf.ru