filmov
tv
Second Partial Derivative Test, Conceptually | Multivariable Calculus

Показать описание
This calculus 3 video will go into the second partial derivative test for finding minimums, maximums, or saddle points of a multivariable function of two or more input variables. Mostly conceptual explanation.
Multi-variable Optimization & the Second Derivative Test
Second Partial Derivative Test, Conceptually | Multivariable Calculus
Explanation of the second derivative test for multivariable functions
second derivative test for multivariable functions example
Partial Derivative and Second Derivative Test for Multivariable Extrema
10.7-1 - First and Second Derivative Tests
Introduction to Second Partial Derivatives
The Second Partials Test Calculus 3
Second derivative test for multivariable function
What does the second derivative actually do in math and physics?
Quadratic Approximation and the Second Partial Derivatives Test
L18 - Max, Min, Saddle Points - Second Derivative Test || Multivariable Calculus
Second derivative test: two variables
Second Derivative Test
Local extrema and saddle points of a multivariable function (KristaKingMath)
Partial derivatives, tangent plane, gradient, and the second partial derivative test
Partial Derivatives
Partial Derivatives Made Simple: A Beginner’s Guide to Multivariable Calculus
📚 How to find the second partial derivative of a function
Second Derivative Test
First and Second Partial Derivatives
Partial Derivative Examples
Unit 21-6 The Mixed Second Derivatives, Estimating from Contour Diagrams - MATH 121
Partial Derivatives - 2nd order Partial Derivatives - Kinetic Energy - Calculus
Комментарии
 0:13:36
0:13:36
 0:15:04
0:15:04
 0:29:35
0:29:35
 0:10:26
0:10:26
 0:16:06
0:16:06
 0:04:35
0:04:35
 0:08:04
0:08:04
 0:10:47
0:10:47
 0:27:56
0:27:56
 0:15:19
0:15:19
 0:22:43
0:22:43
 0:27:16
0:27:16
 0:27:10
0:27:10
 0:12:48
0:12:48
 0:11:23
0:11:23
 0:48:10
0:48:10
 0:10:18
0:10:18
 0:10:21
0:10:21
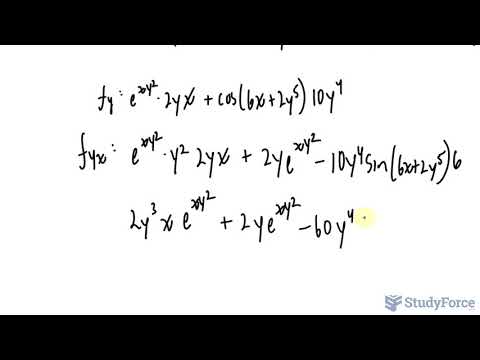 0:05:47
0:05:47
 0:14:08
0:14:08
 0:11:15
0:11:15
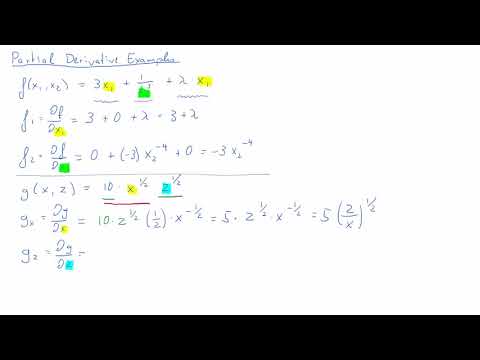 0:07:07
0:07:07
 0:14:39
0:14:39
 0:03:50
0:03:50