filmov
tv
Visual Group Thoery, Lecture 5.5: p-groups

Показать описание
Visual Group Thoery, Lecture 5.5: p-groups
Before we can introduce the Sylow theorems, we need to develop some theory about groups of prime power order, which we call p-groups. In this lecture, we show that the number of fixed point of a p-group acting on a set S is congruent modulo p to |S|. Next, we state and prove the two-part "normalizer lemma". The first part says that for any p-group H, the index [N(H):H] is congruent to [G:H] modulo p. The second part says that if H is not a maximal p-group, then [N(H):H] is a multiple of p.
Before we can introduce the Sylow theorems, we need to develop some theory about groups of prime power order, which we call p-groups. In this lecture, we show that the number of fixed point of a p-group acting on a set S is congruent modulo p to |S|. Next, we state and prove the two-part "normalizer lemma". The first part says that for any p-group H, the index [N(H):H] is congruent to [G:H] modulo p. The second part says that if H is not a maximal p-group, then [N(H):H] is a multiple of p.
Visual Group Theory, Lecture 5.7: Finite simple groups
Research Discussion on Graphs and Groups - Lecture 5
Be Lazy
Cosplay by b.tech final year at IIT Kharagpur
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Visual Group Theory, Lecture 5.1: Groups acting on sets
Visual Group Theory, Lecture 5.3: Examples of group actions
Visual Group Theory, Lecture 6.6: The fundamental theorem of Galois theory
IQ TEST
Visual Group Theory, Lecture 4.5: The isomorphism theorems
Hydrophobic Club Moss Spores
Visual Group Theory, Lecture 5.2: The orbit-stabilizer theorem
Ethnomathematics Lecture 5: Color Symmetries
Most💯 Important Step Before any Procedure 🔥
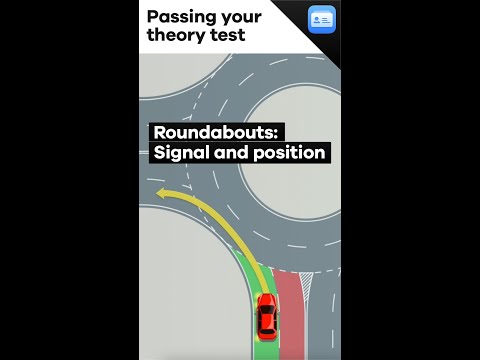
How to signal and position at a UK roundabout
#abacus #smallkid #mentalmath #imagination whats App 9899698414
Top 5 Communication Skills Lessons
#superclever #superznalac #mentalarithmetic #math #franchise #abacuslearning #abacus #education
Reflection of light 💡| Power Of Light Reflection | Experiment with reflection of light #shorts
6 million years of Human Evolution in 40 seconds | HD |
Visual Group Theory, Lecture 1.6: The formal definition of a group
Logical Reasoning Day Trick
What is a vector?
How To Calculate Percents In 5 Seconds
Комментарии
 0:36:34
0:36:34
 1:06:34
1:06:34
 0:00:44
0:00:44
 0:00:15
0:00:15
 0:00:38
0:00:38
 0:32:35
0:32:35
 0:44:05
0:44:05
 0:31:29
0:31:29
 0:00:29
0:00:29
 0:46:19
0:46:19
 0:00:31
0:00:31
 0:27:41
0:27:41
 1:01:54
1:01:54
 0:00:16
0:00:16
 0:00:47
0:00:47
 0:00:17
0:00:17
 0:01:00
0:01:00
 0:00:26
0:00:26
 0:00:19
0:00:19
 0:00:48
0:00:48
 0:12:48
0:12:48
 0:00:34
0:00:34
 0:00:26
0:00:26
 0:00:23
0:00:23