filmov
tv
Why Sums And Averages Tend To Look Gaussian

Показать описание
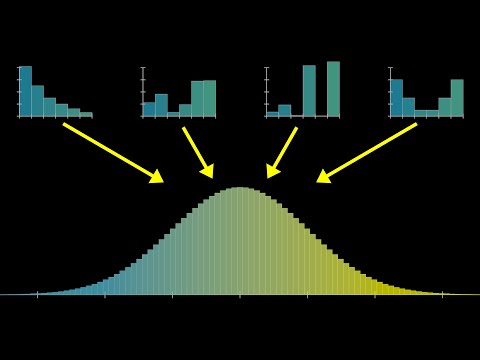
We study the distribution of sums and averages of independent random variables. We show that for both discrete and continuous variables the distribution is obtained via convolution of the corresponding probability mass functions or probability density functions. These repeated convolutions smooth the pmfs and pds making them Gaussian-like, as we illustrate through two examples. In addition, we show that the convolution of two Gaussians is Gaussian (so sums of independent Gaussians are also Gaussian).
Why Sums And Averages Tend To Look Gaussian
11. Riemann Sums and Average Value
But what is the Central Limit Theorem?
The Standard Deviation (and Variance) Explained in One Minute: From Concept to Definition & Form...
NEWYES Calculator VS Casio calculator
How to use basic sums, average, count functions in LibreOffice Calc
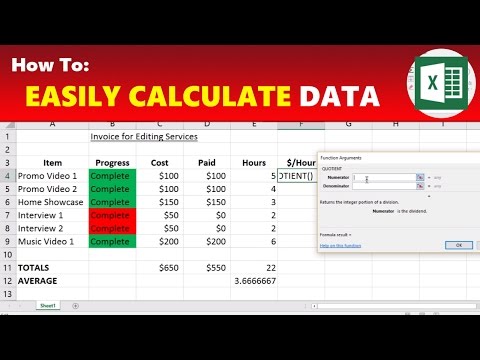
How To: Calculate Sums, Averages, Hourly Rates & Other Functions in Microsoft Excel
Arithmetic progression Formula #Maths #shorts #mathematics
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
SUM AND AVERAGES IN STATISTIC
Why the Strangest Sums in Math Are Actually Useful!
More on sums of independent random variables (Part 1)
One minus one plus one minus one - Numberphile
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Central Limit Theorem for Means and Sums
JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts
😁 Playing 🐍Snake🐍 game on calculator 😜 [official video] #shorts #viral #casio
Statistical Mechanics Lecture 3
What is the Window function in Tableau? Part1 Tableau Functions
Can you find the 5th arrow? #shorts
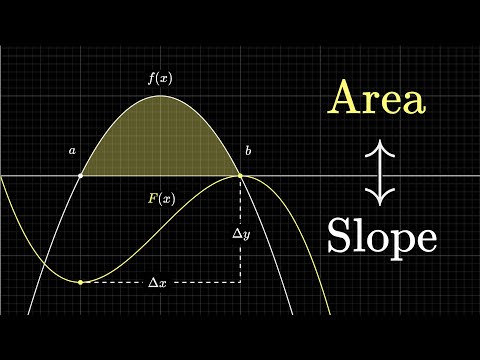
What does area have to do with slope? | Chapter 9, Essence of calculus
Warren Buffett: How to Invest Tiny Sums Of Money During Overvalued 2024 Market
CAT Preparation - Averages Question 3
What is the Ultraviolet Catastrophe?
Комментарии
 0:32:18
0:32:18
 0:37:40
0:37:40
 0:31:15
0:31:15
 0:01:47
0:01:47
 0:00:14
0:00:14
 0:13:09
0:13:09
 0:10:57
0:10:57
 0:00:17
0:00:17
 0:07:50
0:07:50
 0:08:15
0:08:15
 0:10:25
0:10:25
 0:07:51
0:07:51
 0:11:10
0:11:10
 0:00:12
0:00:12
 0:29:16
0:29:16
 0:00:12
0:00:12
 0:00:47
0:00:47
 1:53:27
1:53:27
 0:31:45
0:31:45
 0:00:33
0:00:33
 0:12:39
0:12:39
 0:12:31
0:12:31
 0:04:14
0:04:14
 0:40:29
0:40:29