filmov
tv
G-5. Breadth-First Search (BFS) | C++ and Java | Traversal Technique in Graphs

Показать описание
Find DSA, LLD, OOPs, Core Subjects, 1000+ Premium Questions company wise, Aptitude, SQL, AI doubt support and many other features that will help you to stay focussed inside one platform under one affordable subscription. Have a hassle free one stop solution for up-skilling and preparing.
Checkout the problem link 👇🏼
Breadth-First Search (BFS) | C++ and Java | Traversal Technique in Graphs
G-5. Breadth-First Search (BFS) | C++ and Java | Traversal Technique in Graphs
5.1 Graph Traversals - BFS & DFS -Breadth First Search and Depth First Search
Breadth First Search (BFS): Visualized and Explained
Breadth First Search Algorithm | Shortest Path | Graph Theory
BFS | Breadth First Search #animation
Ch 2.9 :BFS : Breadth-first search ,BFS forest ,BFS Algorithm , Running Time
JavaScript Data Structures - 37 - Binary Search Tree Breadth First Search
6.2 BFS and DFS Graph Traversals| Breadth First Search and Depth First Search | Data structures
Breadth First Search (BFS) Algorithm Explained + Python Implementation
bfs vs dfs in graph #dsa #bfs #dfs #graphtraversal #graph #cse
Breadth-First Search (BFS) | Traversal Technique in Graphs
BFS Algorithm | Breadth First Search Algorithm for Graph Search
Breadth First Search (BFS): How to BURN DOWN a graph to traverse it
Breadth First Search (BFS) with example | Uninformed Search | Artificial Intelligence
Breadth First Search Algorithm Explained With C++ Examples
Depth First Search (DFS) and Breadth First Search (BFS) #dfs #bfs #ai #ml #webdev #html #coding #css
L-4.15: BFS & DFS | Breadth First Search | Depth First Search | Graph Traversing | DAA
Breadth First Search Explained and Implemented in Java | BFS | Graph Traversal & Theory | Geekif...
5. Breadth First Search (BFS) | Trees & Graphs | Bharat Singla
Breadth First Search - Finding Shortest Paths in Unweighted Graphs
Breadth-First Search Algorithm Solved Example Advantages and Disadvantages by Dr. Mahesh Huddar
Depth-first search in 4 minutes
Discrete Math II - 11.4.2 Spanning Trees - Breadth First Search
BFS Algorithm | Breadth First Search in Graph | BFS Traversal | BFS Graph | DSA-One Course #75
Комментарии
 0:19:39
0:19:39
 0:18:31
0:18:31
 0:10:41
0:10:41
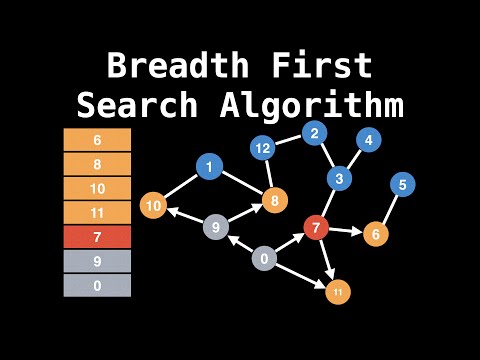 0:07:23
0:07:23
 0:00:20
0:00:20
 0:06:25
0:06:25
 0:05:32
0:05:32
 0:20:27
0:20:27
 0:00:41
0:00:41
 0:00:13
0:00:13
 0:20:43
0:20:43
 0:14:04
0:14:04
 0:16:48
0:16:48
 0:12:57
0:12:57
 0:02:14
0:02:14
 0:00:20
0:00:20
 0:11:16
0:11:16
 0:06:22
0:06:22
 0:15:09
0:15:09
 0:14:23
0:14:23
 0:07:17
0:07:17
 0:04:01
0:04:01
 0:04:57
0:04:57
 0:13:10
0:13:10