filmov
tv
Tricky Exponential Problem

Показать описание
Tricky Exponential Problem
China | Can You Solve This | A Tricky Exponential Problem
China | Can You Solve This | A Tricky Exponential Problem
A Tricky Exponential Problem
China | Can You Solve This | A Tricky Exponential Problem
Can you solve this tricky exponential equation?
China | Can You Solve This | A Tricky Exponential Problem
Solve This Tricky Exponential Equation!
Can You Solve this? | Nice Exponential Problem | Math Olympiad Question |
Maths olympiad | A tricky Exponential Expression solutions | Algebra problem |
Solve The Exponential Equation || X=? || Tricky Exponential Problem...
Tricky Exponent Problem | Only Geniuses Can Solve This Exponential Equation!
tricky Exponential problem
tricky Exponential problem
Can you solve this tricky exponential equation?
Tricky but easy exponential problem | Olympiad Mathematics
A Tricky Exponential Problem | Can You Solve This?
tricky exponential problem
Tricky Exponential Math Problem. #shorts #MathShorts
A Tricky Exponential Problem
How Do We Solve This Tricky Math problem? #maths #exponential #matholympiadquestion
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Tricky exponential math problem #maths #algebra #math #mathstricks
A Very Tricky Exponential Equation With A Quadratic Exponent | Algebra | Math Olympiad
Комментарии
 0:00:55
0:00:55
 0:05:44
0:05:44
 0:06:14
0:06:14
 0:04:44
0:04:44
 0:08:32
0:08:32
 0:11:12
0:11:12
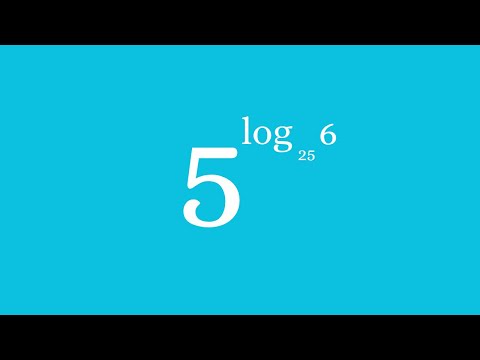 0:09:01
0:09:01
 0:00:24
0:00:24
 0:07:48
0:07:48
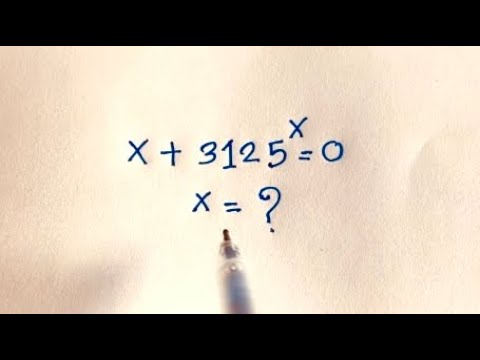 0:10:31
0:10:31
 0:05:50
0:05:50
 0:02:31
0:02:31
 0:00:24
0:00:24
 0:00:24
0:00:24
 0:09:18
0:09:18
 0:02:20
0:02:20
 0:04:42
0:04:42
 0:00:28
0:00:28
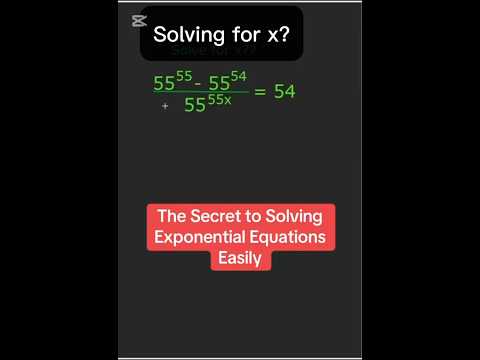 0:01:27
0:01:27
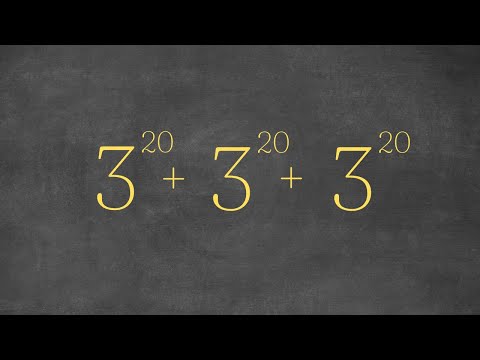 0:10:55
0:10:55
 0:00:53
0:00:53
 0:00:52
0:00:52
 0:00:38
0:00:38
 0:10:25
0:10:25