filmov
tv
Evaluate the limit as x approaches 0 of ((2 + h)^3 -8)/h

Показать описание
How To Find The Limit At Infinity
Evaluating Limits By Factoring
How to Find Any Limit (NancyPi)
Calculus 1 - Introduction to Limits
Learn how to evaluate a limit at infinity
Limit of x/(x^2 + 7x) as x approaches 0
Evaluate the limit as x approaches 5 of (x^2-5x+6)/(x-5)
Infinite Limit Shortcut!! (Calculus)
how can find limit #limit #calculus #maths
Limit of |x|/x as x approaches 0 Does Not Exist | Calculus 1
Evaluate the limit as x approaches 4 of (x^2- 4x)/(x^2-3x-4)
Limits of Multivariable Functions - Calculus 3
Evaluate the limit as x approaches infinity of (1 + a/x)^(bx). l’Hopital’s Rule
Limits at Infinity
Finding Limits an Algebraic Approach
Evaluate the limit as x approaches 2 of x²-4/x-2
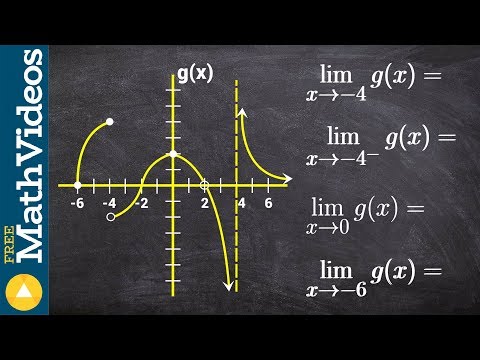
Evaluate all the limits from a given graph
Use Continuity to Evaluate a Limit
Evaluate the limit as x approaches 0^+ for (x ln x). l’Hopital’s Rule
Evaluate the limit as x approaches infinity of (e^x + x)^(1/x). l’Hopital’s Rule
Find the Limit of (2 - x)/(x - 1)^2 as x approaches 1
Evaluate the limit as x approaches 1 of x^(1/(1-x)). l’Hopital’s Rule
How To Evaluate Limits From a Graph
How to Find the Limit at Infinity (NancyPi)
Комментарии
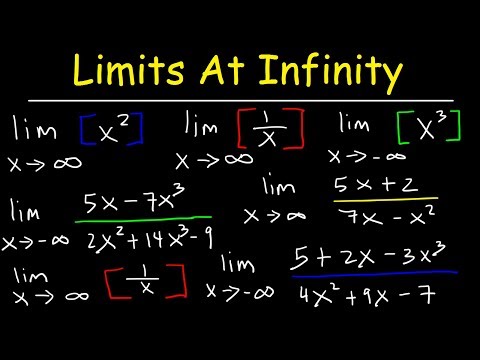 0:13:14
0:13:14
 0:11:35
0:11:35
 0:16:42
0:16:42
 0:20:20
0:20:20
 0:01:40
0:01:40
 0:01:49
0:01:49
 0:01:46
0:01:46
 0:00:51
0:00:51
 0:00:06
0:00:06
 0:05:03
0:05:03
 0:02:19
0:02:19
 0:19:04
0:19:04
 0:05:24
0:05:24
 0:09:54
0:09:54
 0:07:41
0:07:41
 0:02:10
0:02:10
 0:05:34
0:05:34
 0:01:32
0:01:32
 0:02:18
0:02:18
 0:05:00
0:05:00
 0:02:18
0:02:18
 0:03:32
0:03:32
 0:11:32
0:11:32
 0:30:49
0:30:49