filmov
tv
Simplifying Rational Expressions Part 1

Показать описание
This lesson shows how to simplify rational expressions. This is the first part of a two part lesson. This was a lesson created for the MCR3U Functions course in the province of Ontario, Canada.
Simplifying Rational Expressions Part 1
Simplifying Rational Expressions
MCR3U - Simplifying Rational Expressions Part 1 - Grade 11 Functions
06 - Simplifying Rational Expressions in Algebra, Part 1
Simplifying Rational Expressions 1 (old)
Simplifying rational expressions introduction | Algebra II | Khan Academy
Simplifying Rational Expressions... How? (NancyPi)
KutaSoftware: Algebra 1- Simplifying Rational Expressions Part 1
Class 9 Math Exercise 4.4 Complete || 9 Class Mathematics Exercise 4.4 Question No.1 To 6
14 - Multiplying, Dividing & Simplifying Rational Expressions, Part 1
How to Simplify Rational Expressions in Algebra
17 - Adding, Subtracting & Simplifying Rational Expressions, Part 1
Rational Expressions - Basic Introduction
❖ Rational Expressions: Writing in Lowest Terms - Ex 1 ❖
Simplify Rational Expressions Part 1
Simplifying Rational Expressions
Simplifying Rational Expressions, Part One
Simplifying Rational Algebraic Expression - Made Easy
Simplify a rational expression
How to Simplify Rational Expressions
Simplifying Rational Expressions
Ex 1: Simplifying Rational Expressions - Monomials
How to simplify a rational expression using factoring
Rational Expressions: Simplify (x^2 - 1)/(x + 1)
Комментарии
 0:11:08
0:11:08
 0:07:54
0:07:54
 0:37:43
0:37:43
 0:03:39
0:03:39
 0:07:28
0:07:28
 0:14:04
0:14:04
 0:10:09
0:10:09
 0:24:10
0:24:10
 0:26:55
0:26:55
 0:01:00
0:01:00
 0:22:24
0:22:24
 0:12:46
0:12:46
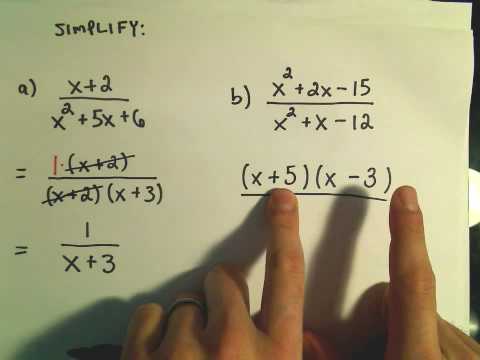 0:05:24
0:05:24
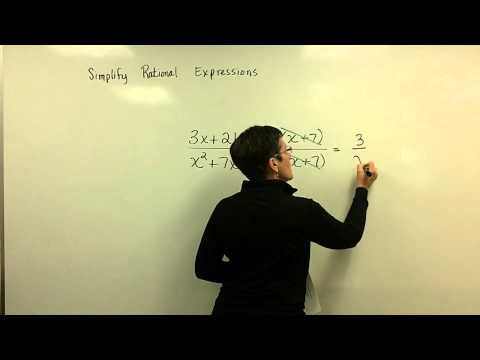 0:10:11
0:10:11
 0:08:19
0:08:19
 0:04:12
0:04:12
 0:07:00
0:07:00
 0:07:47
0:07:47
 0:00:59
0:00:59
 0:18:27
0:18:27
 0:04:57
0:04:57
 0:01:30
0:01:30
 0:00:21
0:00:21