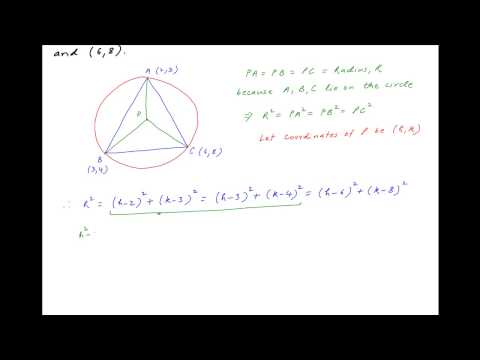
Find Equation of Circle Inscribed in a Triangle Formed by Intersection of Three Lines

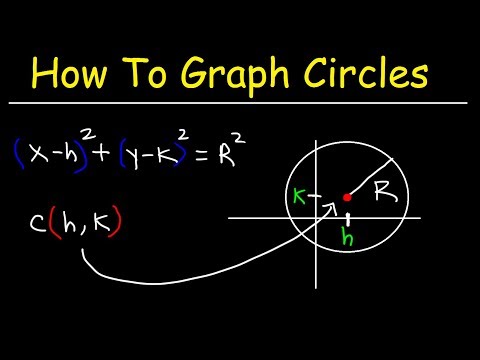
Circumcenter of a triangle is the point of intersection of the right bisector of the three sides of a triangle. All the three vertices are same distance away from the circumcentre and so a circle can be drawn circumscribing the triangle using this point as the centre. Orthocentre of a triangle is a point where the perpendiculars drawn from each vertex to the opposite sides intersect. For an acute angle triangle, the orthocenter is inside the triangle; for right triangle it is on the hypotenuse and for the obtuse angle triangle it lies outside the triangle. Incentre of a triangle is the point of intersection of three interior angles of a triangle. A circle inscribed in a triangle can be drawn with center at the incenter.
#mpm2d_geometry #sat_act_tutor #mpm2d_areaoftriangle #analyticgeometry #coordinategeometryclass10