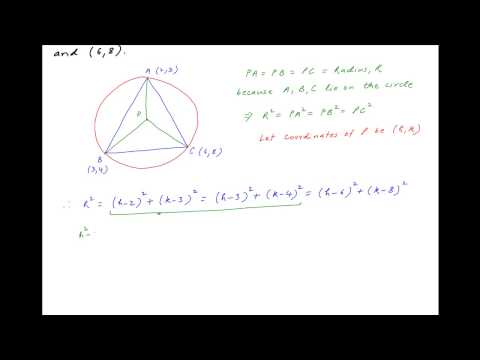
Find center of circle circumscribing a triangle with vertices (2,3), (3,4) and (6,8).

preview_player
Показать описание
  1. mathmuni
  2. Mathematics
  3. Maths
  4. solution
  5. IIT
  6. JEE
Рекомендации по теме
Find center of 0:04:43

Find center of circle circumscribing a triangle with vertices (2,3), (3,4) and (6,8).

EGD Circumscribed Circle 0:02:46

EGD Circumscribed Circle

Inscribed and Circumscribed 0:01:46

Inscribed and Circumscribed Circles of a Triangle. Geometry video.

Compass Tips - 0:00:31

Compass Tips - Find Center of a Circle 2

Can you find 0:10:25

Can you find the Radius of the circle? | (Triangle inscribed in a circle) | #math #maths

Find area of 0:08:05

Find area of the circumscribed circle of an isosceles triangle | Important Geometry skills explained

Given a Circle 0:04:31

Given a Circle Inscribed in a Triangle, Find the Radius of the Circle.

How to draw 0:02:22

How to draw a circumcircle of an equilateral triangle

Easiest Way To 0:02:32

Easiest Way To Find The Center Of A Circle.

Find the Center 0:03:52

Find the Center of a Circle the Easy Way

Find the Center 0:06:38

Find the Center of a Circle (3 EASY and QUICK Ways)

Circumcircle of a 0:01:00

Circumcircle of a Triangle #jeedailyconcepts #trigonometry

How to find 0:02:41

How to find the coordinates of the center of the circumscribed circle: JEE | JEE Prep | Geometry

Show that P(1,−1) 0:05:53

Show that P(1,−1) is the centre of the circle circumscribing the triangle A(4,3),B(−2,3) & C(6,...

Construct a Circle 0:01:15

Construct a Circle Circumscribed around a Given Triangle

Coordinates of the 0:02:34

Coordinates of the center and length of the radius of circle circumscribed about a right triangle.

EGD Inscribed Circle 0:02:14

EGD Inscribed Circle

XI Conic Sections 0:09:03

XI Conic Sections Find the equation of the circle circumscribing the triangle formed by the lines x

Find the Radius 0:03:42

Find the Radius of inscribed circle using Area and sides of Triangle | Find the Radius of circle

Find the coordinates 0:05:40

Find the coordinates of the center of the circle inscribed in a triangle whose vertices are (-...

C16--Construct a Circumscribed 0:02:34

C16--Construct a Circumscribed Circle Around a Triangle

How To Find 0:06:12

How To Find The Center Of A Circle Using A Square

How to draw 0:05:41

How to draw the Incenter and the Inscribed Circle of a triangle

How to add 0:03:59

How to add circle around a character in MS Word, how to enclose an alphabet by a circle Word

Комментарии
Автор

Thank you bossulica! It helped a lot! Just good!!

IaminCiora-vggh
Автор

Great question! The center of a circle circumscribing a triangle can indeed lie outside the triangle. Consider a simple example: The center of the circle square(x)+square(y)=2 is the origin. Consider a triangle formed by three points on this circle (1, 1), (-1, 1) and (0, sqrt2). The center (0, 0) of the circumscribing circle clearly lies outside the triangle. The problem in this video is similar. Plotting to scale (which I have not done in my explanation) will help make it clearer. Hope this helps.

mathmuni
Автор

Where the crap did the 6 come from that you threw in there? I got everything, right up until that point.... I get why it is there, but where did it come from?

shawnonmariescott
Автор

do the points really create a triangle? because i graphed it but i only got a straight line :/

burning_chain
Автор

Anyone can answer, where did he get the (6h + 6k) and -6×6?

marlynamora
Автор

Sir I didn't understand, what did u do from 3:35

bandanashah
Автор

but then the center of the circle would be outside of the circle tho???
im so confused

jindo
Автор

This is so hard to understand. Numbers from next equation just pop up before our eyes without further explanation.

aogavin
Автор

Wow nice one or made me to do mathematical operation easily

kamalrajjoshi
Автор

please make the video a little faster :(

huntertran