filmov
tv
How to Expand x+1 Raised to an Irrational Power

Показать описание
If n is a natural number, (x+1)^n can be easily expanded, but how can we expand it when it is raised to a general real power?
[BGM]
[Materials]
VOICEVOX:ずんだもん (Zundamon, illustrated by sakamoto_AHR)
VOICEVOX:四国めたん (Shikoku Metan, illustrated by sakamoto_AHR)
(+ other tools)
pixabay
This video uses synthesized voices.
#math
[BGM]
[Materials]
VOICEVOX:ずんだもん (Zundamon, illustrated by sakamoto_AHR)
VOICEVOX:四国めたん (Shikoku Metan, illustrated by sakamoto_AHR)
(+ other tools)
pixabay
This video uses synthesized voices.
#math
How to Expand x+1 Raised to an Irrational Power
How to expand a binomial raised to the 3 power
Use binomial expansion to expand a binomial to the fourth power
Binomial Expansion with Negative exponent
Expanding Brackets
Expand & Simplify: (x + 1)^2
Using binomial expansion to expand a binomial to the fourth degree
Expand & Simplify: (x - 1)^2
Expand & Simplify: (x - 1)^3
binomial theorem expansion form #math #binomial#ncert
Binomial Expansion wilth fractional exponent | lesson 2
Expand using Binomial Theorem #mathshorts
Expand & Simplify: (x + 2)(x + 1)
Tips on Expanding a Binomial Using Pascal’s Triangle
Expand & Simplify: (x - 1)(x + 1)
Expand a binomial to the fifth power using pascals triangle
nth term of Binomial Expansion | General Formula
Learn how to expand a binomial to fourth power by multiplying
The Binomial Theorem : Fractional Powers : Expanding (1-2x)^1/3
Binomial Expansion | Fractional Exponent.
Factoring Prep | Expand and Simplify (Grade 10)
Expand & Simplify: (x - 1)(x - 2)
Human Calculator Solves World’s Longest Math Problem #shorts
23 - The Binomial Theorem & Binomial Expansion - Part 1
Комментарии
 0:11:10
0:11:10
 0:02:53
0:02:53
 0:04:44
0:04:44
 0:03:32
0:03:32
 0:00:51
0:00:51
 0:01:36
0:01:36
 0:06:27
0:06:27
 0:01:38
0:01:38
 0:02:49
0:02:49
 0:00:38
0:00:38
 0:08:02
0:08:02
 0:00:58
0:00:58
 0:01:37
0:01:37
 0:01:01
0:01:01
 0:01:06
0:01:06
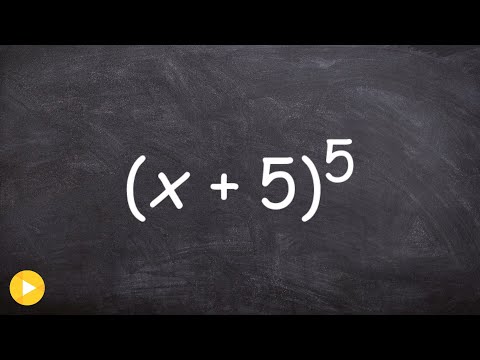 0:03:17
0:03:17
 0:12:02
0:12:02
 0:03:50
0:03:50
 0:04:45
0:04:45
 0:05:57
0:05:57
 0:22:51
0:22:51
 0:01:08
0:01:08
 0:00:34
0:00:34
 0:34:02
0:34:02