filmov
tv
The Role of Proofs in MIP* = RE | Quantum Colloquium
Показать описание
Henry Yuen (Columbia University)
Quantum Colloquium, May. 4th, 2021
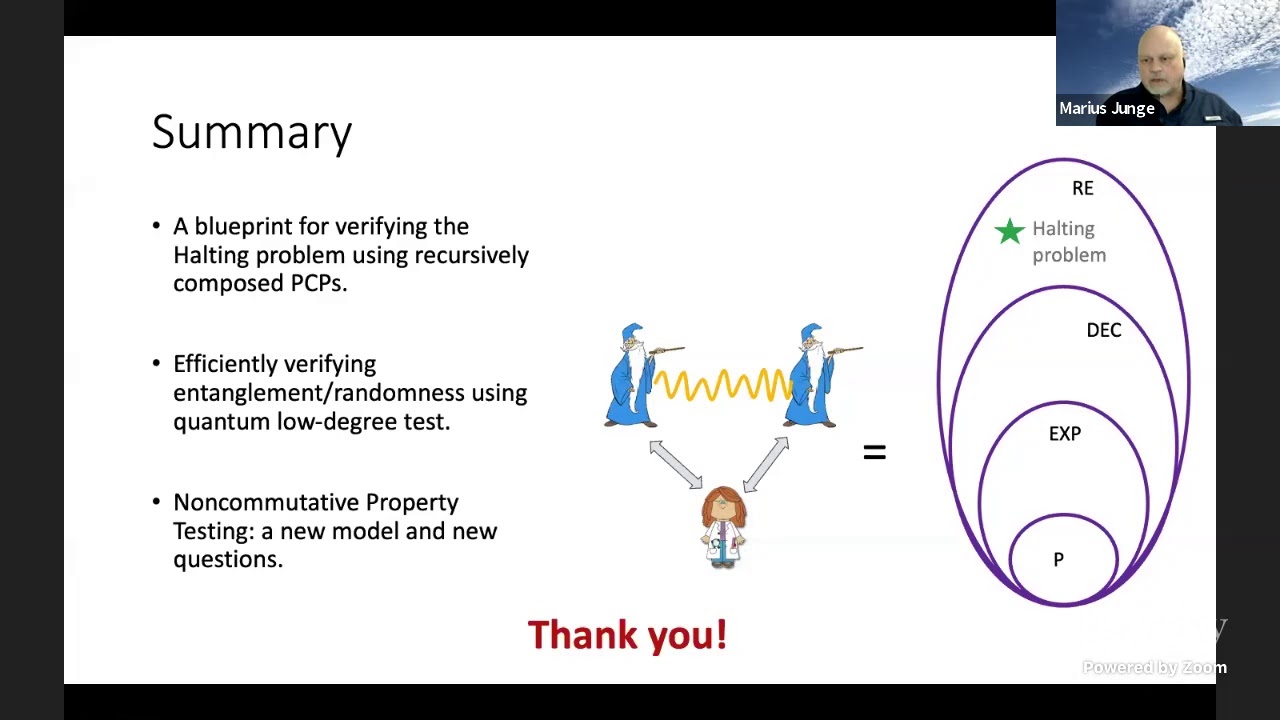
MIP* = RE has the startling consequence that, in the entangled provers model, there is an interactive proof for the Halting problem. In other words, for all Turing machines M that halt, two separated but quantum entangled provers can convince a classical verifier that M eventually terminates --- and furthermore the complexity of the verifier does not depend on the running time of M!
What does it mean to have an interactive proof for an undecidable problem, and how does quantum entanglement enable this mind-boggling leap in complexity for multiprover interactive proofs? In this talk, I will try to shed light on these questions by highlighting the central role of proofs in MIP* = RE: at its core, the MIP* protocol for the Halting problem recursively combines proofs of both classical and quantum properties. Time permitting, I will also discuss how the techniques in MIP* = RE point to a broader set of questions about "noncommutative property testing."
Based on joint work with Zhengfeng Ji, Anand Natarajan, Thomas Vidick, and John Wright.
Quantum Colloquium, May. 4th, 2021
MIP* = RE has the startling consequence that, in the entangled provers model, there is an interactive proof for the Halting problem. In other words, for all Turing machines M that halt, two separated but quantum entangled provers can convince a classical verifier that M eventually terminates --- and furthermore the complexity of the verifier does not depend on the running time of M!
What does it mean to have an interactive proof for an undecidable problem, and how does quantum entanglement enable this mind-boggling leap in complexity for multiprover interactive proofs? In this talk, I will try to shed light on these questions by highlighting the central role of proofs in MIP* = RE: at its core, the MIP* protocol for the Halting problem recursively combines proofs of both classical and quantum properties. Time permitting, I will also discuss how the techniques in MIP* = RE point to a broader set of questions about "noncommutative property testing."
Based on joint work with Zhengfeng Ji, Anand Natarajan, Thomas Vidick, and John Wright.
An Introduction to Mathematical Proofs
The Role of Proofs in MIP* = RE | Quantum Colloquium
Learn to Write Mathematical Proofs
Panel Discussion on The Role of Proofs in MIP* = RE | Quantum Colloquium
How To Figure Out Math Proofs On Your Own
The paradox at the heart of mathematics: Gödel's Incompleteness Theorem - Marcus du Sautoy
The Importance of Maths Proofs for Children
When Computers Write Proofs, What's the Point of Mathematicians?
Important Proofs in Mathematics; Trigonometry; Law Sine : - 14. #lawofsine #trigonometry #proof
Discrete Math Proofs in 22 Minutes (5 Types, 9 Examples)
Proofs made easy
Proof of Logarithmic derivative #maths
Advice For Writing Math Proofs
proofs involving functions -- proof writing examples 18
1.11 Proofs: an example
Proofs with Rules of Inference 1 (Propositional Logic for Linguists 15)
UP TALKS | Proofs in Mathematics
Proof by induction | Sequences, series and induction | Precalculus | Khan Academy
Math proofs be like… #shorts
Indirect Proofs in Algebra and Geometry: Lesson (Basic Geometry Concepts)
Intro to Proofs - Functions
1 = 3 [Bogus Proofs]
Proofs in Mathematics | Dr. Priscilla Macansantos
How to Study Hard Proofs in Numerical Analysis (and Real Analysis)
Комментарии
 0:09:41
0:09:41
 1:02:30
1:02:30
 0:00:15
0:00:15
 0:44:53
0:44:53
 0:09:00
0:09:00
 0:05:20
0:05:20
 0:01:48
0:01:48
 0:06:34
0:06:34
 0:04:10
0:04:10
 0:22:09
0:22:09
 0:12:59
0:12:59
 0:00:23
0:00:23
 0:05:27
0:05:27
 0:13:10
0:13:10
 0:02:56
0:02:56
 0:07:16
0:07:16
 0:27:29
0:27:29
 0:09:23
0:09:23
 0:00:39
0:00:39
 0:03:40
0:03:40
 0:13:15
0:13:15
 0:03:23
0:03:23
 0:27:20
0:27:20
 0:51:04
0:51:04