filmov
tv
A radical equation.
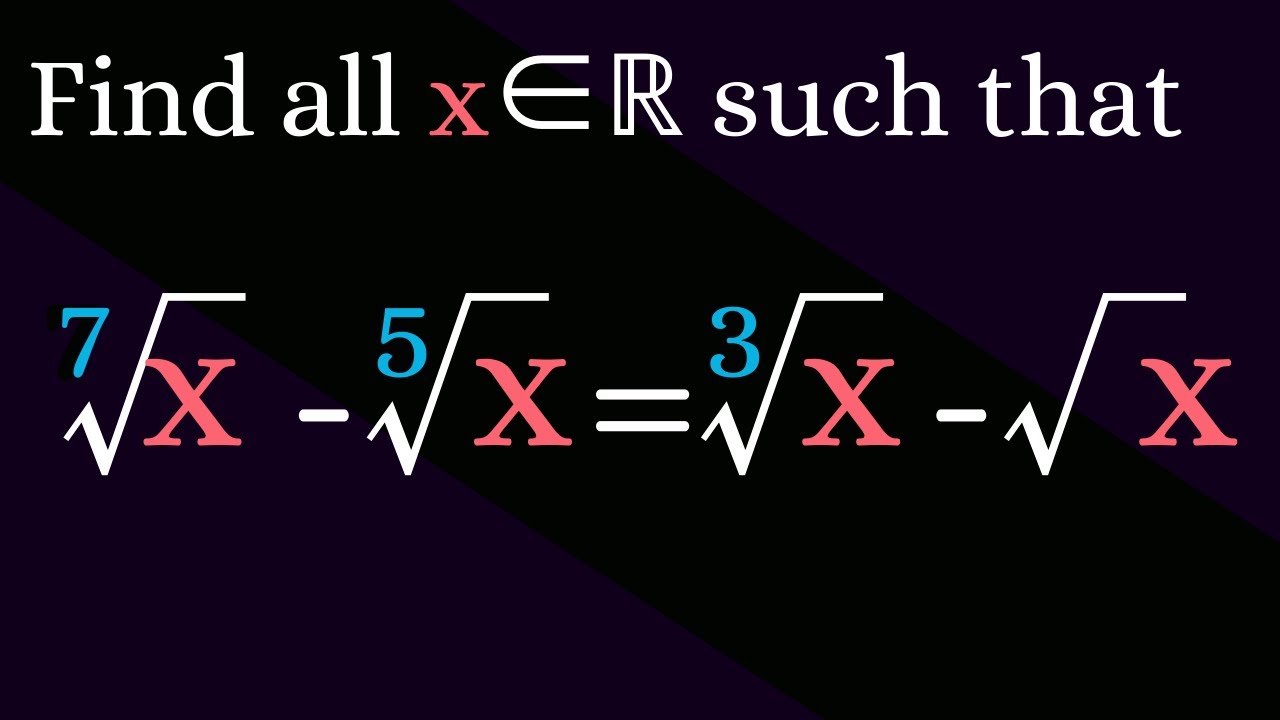
Показать описание
We solve a nice radical equation, using Descartes Rule of signs.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Solving Radical Equations
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Solving a Radical Equation Using Factoring and Checking Your Answers
Radical Equations
Solving Radical Equations | SHS 1 ELECTIVE MATH
Radical equation – each step to solve…
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving Radical Equations
Solving a Symmetric Radical Equation: A Step-by-Step Guide
Simplifying Radicals Easy Method
Learn How to Solve a Radical Equation and Check Your Answers
Solving A Radical Equation #math #algebra #radicals
The most important thing you need to know to solve radical equations
An Infinite Radical Equation
Introduction to solving a radical equation
What Is a Radical Expression in Math? : Radical Numbers
A radical equation.
Can You Solve a Radical Equation?
A Quick and Easy Radical Equation
A Radical Expression | Math Olympiads
Solving Radical Equations (More Challenging)
Equation Challenge: Solve a Radical Equation
How to Solve a Radical Equation with two Square Root Terms
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Комментарии
 0:17:11
0:17:11
 0:18:05
0:18:05
 0:04:25
0:04:25
 0:10:59
0:10:59
 0:11:48
0:11:48
 0:14:34
0:14:34
 0:03:11
0:03:11
 0:03:31
0:03:31
 0:06:50
0:06:50
 0:03:42
0:03:42
 0:03:18
0:03:18
 0:00:46
0:00:46
 0:03:42
0:03:42
 0:04:29
0:04:29
 0:01:00
0:01:00
 0:02:36
0:02:36
 0:13:35
0:13:35
 0:00:31
0:00:31
 0:09:16
0:09:16
 0:00:45
0:00:45
 0:04:14
0:04:14
 0:00:52
0:00:52
 0:04:57
0:04:57
 0:11:20
0:11:20