Calculus 1 - Derivatives and Related Rates (16 of 24) Filling a Semi-Sphereical Bowl V(H2O)=?

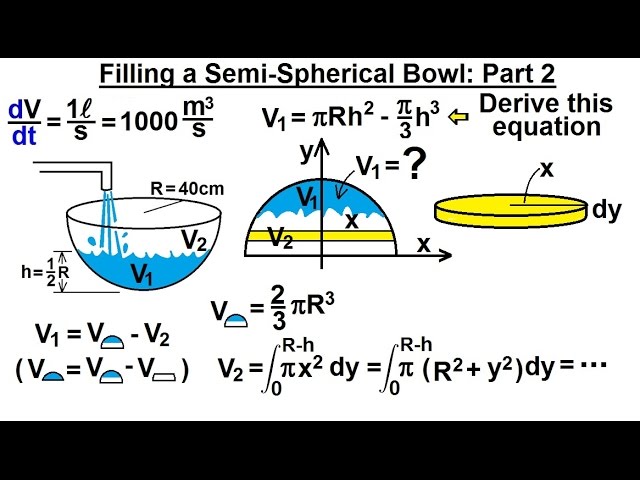
I this video I will derive the volume equation of the water level of a semi-spherical container.

Next video in this series can be seen at:

[joeyborja]

Crystal clear and concise what other teachers could have presented it in hours or not at all!

[ptyptypty]

that derivation was AWESOME!!... thanks for that!!... (still catching up on older videos... ) :)

[logeshtu]

i didn't understand the part x^2+y^2=R, R is always varies at any point y coordinate system (slice of part )
X, Y, R never form the triangle form the point of slice part ?
please explain ?
your teaching superb !!!!, i am fan of your teaching

[subhamoychakraborty]

Sir I have a question. If a circular patch is increasing radially on a sphere how much time would it take to cover the whole sphere? Assuming (dr/dt)= fixed

[tashfeenahmed]

sir have you made videos relating upthrust of water on objects immersed in it?

[baoenlai]

R is the radius isn't it? Then same as X? How come R^2 = X^2 + Y^2? It's not a triangle?

[MrBillbranch]

How can I use this process to arrive at a formula for a section that *does not* start as x=0, let's say x=2 on the x & y axis.