filmov
tv
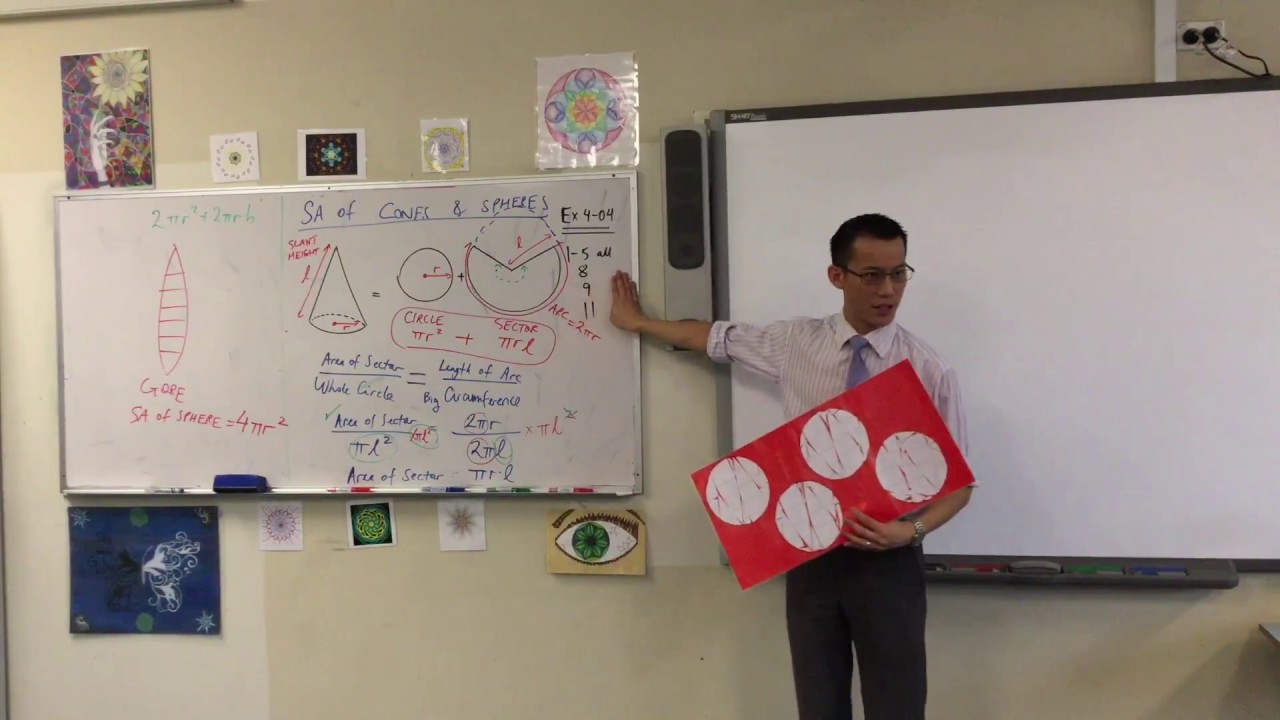
Surface Area of a Cone (2 of 2: Deriving the formula)
Показать описание
Surface Area of a Cone | Math with Mr. J
Volume and Surface Area of a Cone & Lateral Area Formula- Basic Geometry
What is the Surface Area of a Right Circular Cone? | Don't Memorise
Surface Area of a Cone (1 of 2: Understanding the net)
Surface Area of a Cone with Lateral Area - geometry
How to find the surface area of a cone
Surface Area of a Cone - Nerdstudy
Surface Area of a Cone
surface area of cones (KristaKingMath)
Volume and Surface Area of a Cone | Grade 5 Crossover Playlist | GCSE Maths Tutor
Surface Area of a Cone
How to Derive the Surface Area of a Cone Formula Made Super Easy
Surface Area of a Cone Formula Derivation Concept with Visual Easy Approach
SURFACE AREA OF A CONE.
Surface Area of Cones and Pyramids
Surface Area of a Cone – Let’s Figure it out….
Surface Area of a Cone (2 of 2: Deriving the formula)
Surface Area of a Cone
Easy math. Deriving the formula for the volume of a cone #ibmath #igcse #ibexam #math #ipmath
Surface Area of a Cone - Visual Explanation and Example (Mastering Geometry)
Learn how to find the surface area of a cone
Finding The Surface Area Of Cones With And Without The Slant Height
Geometry – Surface Area of Cones
Surface Area of a Right Circular Cone | Part 1/3 | English | Class 9
Комментарии
 0:05:39
0:05:39
 0:13:47
0:13:47
 0:04:34
0:04:34
 0:07:11
0:07:11
 0:03:02
0:03:02
 0:01:44
0:01:44
 0:10:29
0:10:29
 0:01:00
0:01:00
 0:04:46
0:04:46
 0:14:28
0:14:28
 0:01:06
0:01:06
 0:03:42
0:03:42
 0:16:07
0:16:07
 0:05:15
0:05:15
 0:04:33
0:04:33
 0:11:49
0:11:49
 0:09:04
0:09:04
 0:02:42
0:02:42
 0:00:48
0:00:48
 0:06:57
0:06:57
 0:14:18
0:14:18
 0:08:52
0:08:52
 0:05:07
0:05:07
 0:07:36
0:07:36