filmov
tv
When Area equals Perimeter (in numerical value).

Показать описание
Here's a cute little topic: When does a two-dimensional geometric figure have area and perimeter the same numerical value? There are classic examples of integer rectangles and integer right triangles with this property. An email from Jim M. inspired me to push this all a little bit further. (Thank you, Jim!)
When Area equals Perimeter (in numerical value).
Finding the Perimeter
How to Find Length & Width When You Know the Perimeter & Square Area : Math Skills
Perimeter, Area, and Volume Explained | Math with Mr. J
Math Antics - Area
Equal Perimeters and Areas Problem — Circular Sector with Equal Perimeter and Area as Square
Area and Perimeter
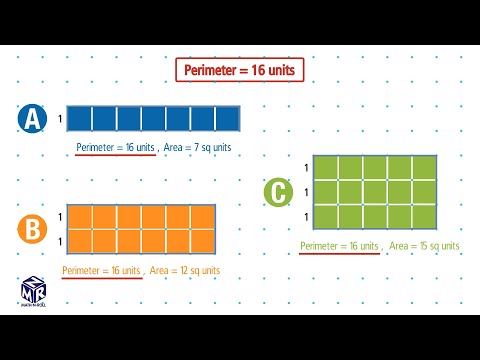
Same Perimeter, Different Areas. Grade 3
What are the dimensions of a rectangle with the area and perimeter shown?
What is perimeter of a Rectangle and how to find it? #math #youtube #mathtrick #shorts #learning
Area and perimeter of square | Ayushi teacher | Area and perimeter #maths #area #perimeter
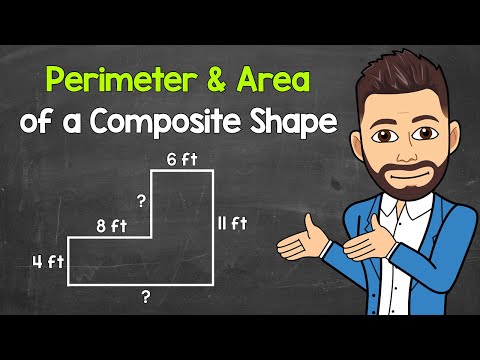
Finding the Perimeter and Area of a Composite Shape | L-Shaped Example | Geometry | Math with Mr. J
Find length and width when area and perimeter of rectangle is given Quadratic Application
Area vs. Perimeter | MightyOwl Math | 3rd Grade
The area of the rectangle is 24, what is the perimeter? (HINT: think quadratic equation)
Area for Kids
Ex: Find the Area of a Rectangle Given the Perimeter
Math Antics - Perimeter
Area and Perimeter Challenge
Why is a Square's area greater than a Rectangle with same Perimeter
Maths - Perimeter using 1cm squares
Is there a triangle with area and perimeter both equal to 12?
When the perimeter and area of a square are numerically equal then the length of the side of square
Find Dimensions Of Rectangle Whose perimeter is 40 inches and whose area is Maximum
Комментарии
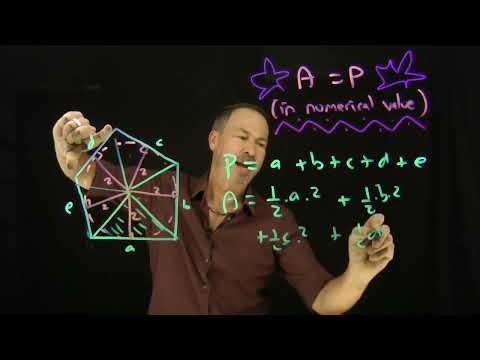 0:14:34
0:14:34
 0:00:40
0:00:40
 0:02:00
0:02:00
 0:10:21
0:10:21
 0:10:26
0:10:26
 0:03:56
0:03:56
 0:17:49
0:17:49
 0:04:29
0:04:29
 0:02:46
0:02:46
 0:00:45
0:00:45
 0:00:16
0:00:16
 0:08:21
0:08:21
 0:04:55
0:04:55
 0:07:06
0:07:06
 0:12:43
0:12:43
 0:08:58
0:08:58
 0:02:25
0:02:25
 0:07:29
0:07:29
 0:00:58
0:00:58
 0:02:44
0:02:44
 0:03:27
0:03:27
 0:09:39
0:09:39
 0:01:14
0:01:14
 0:02:25
0:02:25