filmov
tv
The Most Important Limit In Calculus
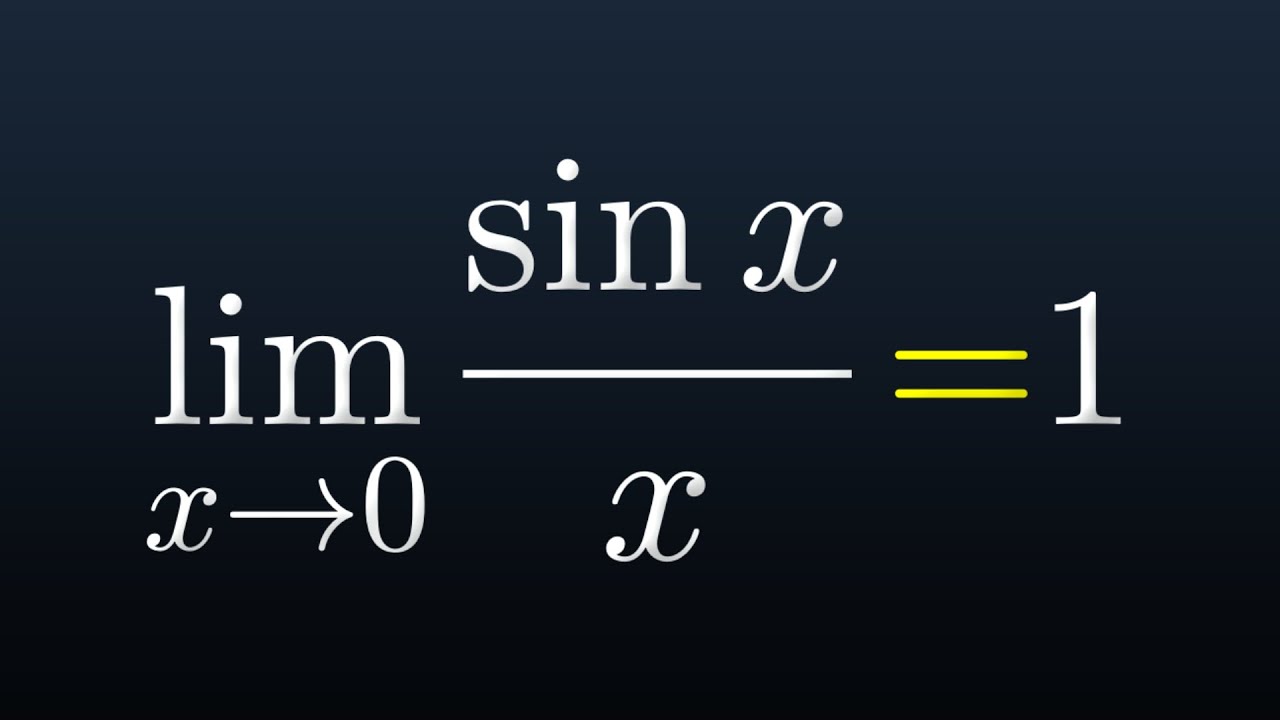
Показать описание
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #limit
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #limit
The Most Important Limit In Calculus
The most important limit in Calculus // Geometric Proof & Applications
the most controversial limit in calculus 1
The Most Important Math Formula For Understanding Physics
How to Find Any Limit (NancyPi)
THE MOST IMPORTANT THING (BY HOWARD MARKS)
The essence of calculus
Definition of the Limit of a Sequence | Real Analysis
#9thmaths #9thclass #maths|Most important Questions Of Polynomials Class-9th Math|Limits 11 R.S.Agga
Understand Calculus in 35 Minutes
What's so special about Euler's number e? | Chapter 5, Essence of calculus
The MOST Important Detail in PADEL that Changed Everything
Limit of a Sequence
What is a Lower Interval Limit? | Q+A #52
The Most Important Economic Schools of Thought | Economics Explained
Attitude - Lion King - Don't Cross The Limit 🦁 👑 #shorts #attitude #status #lionking
limit theta tends to zero sin theta over theta/most important question
limit and limiting value ll class 11/ Ctevt ll math
Real-world application of the Central Limit Theorem (CLT)
Learn Calculus Limit Laws - The Key to Solving Problems | Step-by-Step
What is an Aggregate Limit in a Liability Policy?
Limit of function with Examples
Eagles - Take It To The Limit (Live 1977) (Official Video) [4K]
Skills for Healthy Romantic Relationships | Joanne Davila | TEDxSBU
Комментарии
 0:03:05
0:03:05
 0:11:54
0:11:54
 0:08:19
0:08:19
 0:31:42
0:31:42
 0:16:42
0:16:42
 0:15:09
0:15:09
 0:17:05
0:17:05
 0:13:59
0:13:59
 0:06:16
0:06:16
 0:36:22
0:36:22
 0:13:50
0:13:50
 0:26:04
0:26:04
 0:11:20
0:11:20
 0:12:15
0:12:15
 0:26:05
0:26:05
 0:00:17
0:00:17
 0:22:51
0:22:51
 0:07:48
0:07:48
 0:07:27
0:07:27
 0:16:33
0:16:33
 0:04:11
0:04:11
 0:10:43
0:10:43
 0:05:04
0:05:04
 0:15:53
0:15:53