filmov
tv
SEPARATION BUT MATHEMATICALLY: What Types of Mathematical Topologies are there? | Nathan Dalaklis

Показать описание
The title of this video is a bit convoluted. What do you mean by "Separation but Mathematically"? Well, in this video I'll be giving a (very diluted) answer to the question "What types of mathematical topologies are there?" by introducing the separation axioms in topology.
The separation axioms are additional criteria that one can add to the basic axioms of a topology that guarantee some level of separation between points and sets in a given topological space in point set topology. There are several different separation axioms I'll introduce here and some examples will come up along the way as well. If you want to jump to a specific separation axiom, example, or part of the video I have time carded those here.
00:00 Some Intuition for "why"
03:41 Topological Space and Topology Basics
07:00 Separated Points
07:32 Symmetric Spaces
08:16 Kolmogorov Spaces
08:53 Acccessible Spaces
09:41 Co-Finite Topology
11:11 Hausdorff and PreRegular Spaces
12:58 Regular Hausdorff Spaces
13:31 Normal Hausdorff Spaces
14:00 Urysohn and Completely Hausdorff Spaces
15:41 Co-Countable Extension Topology
16:25 Completely Normal Hausdorff Spaces
17:13 Perfectly Normal Hausdorff Spaces
_____________________
_____________________
Subscriber Count as of release: 1063
#CHALK #PointSetTopology #Topology
The separation axioms are additional criteria that one can add to the basic axioms of a topology that guarantee some level of separation between points and sets in a given topological space in point set topology. There are several different separation axioms I'll introduce here and some examples will come up along the way as well. If you want to jump to a specific separation axiom, example, or part of the video I have time carded those here.
00:00 Some Intuition for "why"
03:41 Topological Space and Topology Basics
07:00 Separated Points
07:32 Symmetric Spaces
08:16 Kolmogorov Spaces
08:53 Acccessible Spaces
09:41 Co-Finite Topology
11:11 Hausdorff and PreRegular Spaces
12:58 Regular Hausdorff Spaces
13:31 Normal Hausdorff Spaces
14:00 Urysohn and Completely Hausdorff Spaces
15:41 Co-Countable Extension Topology
16:25 Completely Normal Hausdorff Spaces
17:13 Perfectly Normal Hausdorff Spaces
_____________________
_____________________
Subscriber Count as of release: 1063
#CHALK #PointSetTopology #Topology
Комментарии
 0:20:01
0:20:01
 0:23:13
0:23:13
 0:00:38
0:00:38
 0:04:50
0:04:50
 0:17:39
0:17:39
 0:00:45
0:00:45
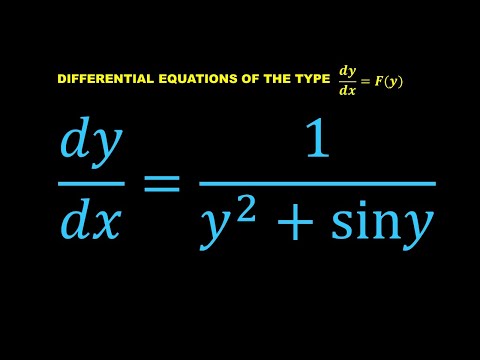 0:01:49
0:01:49
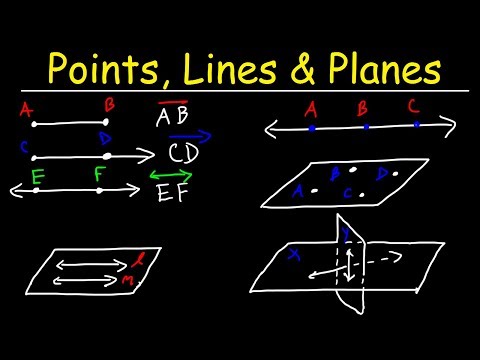 0:14:26
0:14:26
 0:40:45
0:40:45
 0:01:59
0:01:59
 0:01:48
0:01:48
 0:28:17
0:28:17
 0:00:41
0:00:41
 0:22:21
0:22:21
 0:12:18
0:12:18
 0:03:23
0:03:23
 0:00:16
0:00:16
 0:13:30
0:13:30
 0:04:22
0:04:22
 0:00:15
0:00:15
 0:00:56
0:00:56
 0:00:53
0:00:53
 0:04:03
0:04:03
 0:03:16
0:03:16