filmov
tv
Intro to Dimensional Analysis: How Much Energy in an Atomic Bomb? Or a Supernova?

Показать описание
Dimensional Analysis is an extremely useful tool to create mathematical models. It is very simple: Decide what variables your function depends on, and then solve a linear system of equations so you can make at least the dimensions or units of match correctly. This will give you the basic shape, and then with some experimental data you can find the values of the constants. Even though Dimensional Analysis is easy, it is extremely powerful!
This approach was used by Sir G.I. Taylor in 1947 to estimate the energy used in the Trinity test of an atomic bomb. He looked at the video and photos to measure radius and time and decide that the radius would depend on time, energy, and density. Using Dimensional Analysis he would compute the energy correctly within 10%. Amazingly, you can use the same formula to make accurate predictions of the explosions of supernova such as the Tycho Supernova that astronomers saw briefly in 1572.
Tycho Supernova image photo credit: NASA/JPL-Caltech/UCLA
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
This approach was used by Sir G.I. Taylor in 1947 to estimate the energy used in the Trinity test of an atomic bomb. He looked at the video and photos to measure radius and time and decide that the radius would depend on time, energy, and density. Using Dimensional Analysis he would compute the energy correctly within 10%. Amazingly, you can use the same formula to make accurate predictions of the explosions of supernova such as the Tycho Supernova that astronomers saw briefly in 1572.
Tycho Supernova image photo credit: NASA/JPL-Caltech/UCLA
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Комментарии
 0:06:14
0:06:14
 0:15:47
0:15:47
 0:07:46
0:07:46
 1:01:39
1:01:39
 0:04:15
0:04:15
 0:05:13
0:05:13
 0:08:38
0:08:38
 0:13:44
0:13:44
 0:09:48
0:09:48
 0:05:44
0:05:44
 0:13:32
0:13:32
 0:04:41
0:04:41
![[HD] Dimensional Analysis](https://i.ytimg.com/vi/Vyr20KfKKU4/hqdefault.jpg) 0:11:53
0:11:53
 0:36:52
0:36:52
 0:06:42
0:06:42
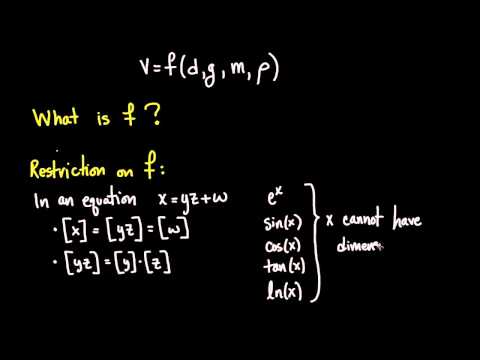 0:18:09
0:18:09
 0:02:05
0:02:05
 0:06:29
0:06:29
 0:38:41
0:38:41
 0:00:43
0:00:43
 0:00:59
0:00:59
 0:12:09
0:12:09
 0:00:11
0:00:11
 0:10:30
0:10:30