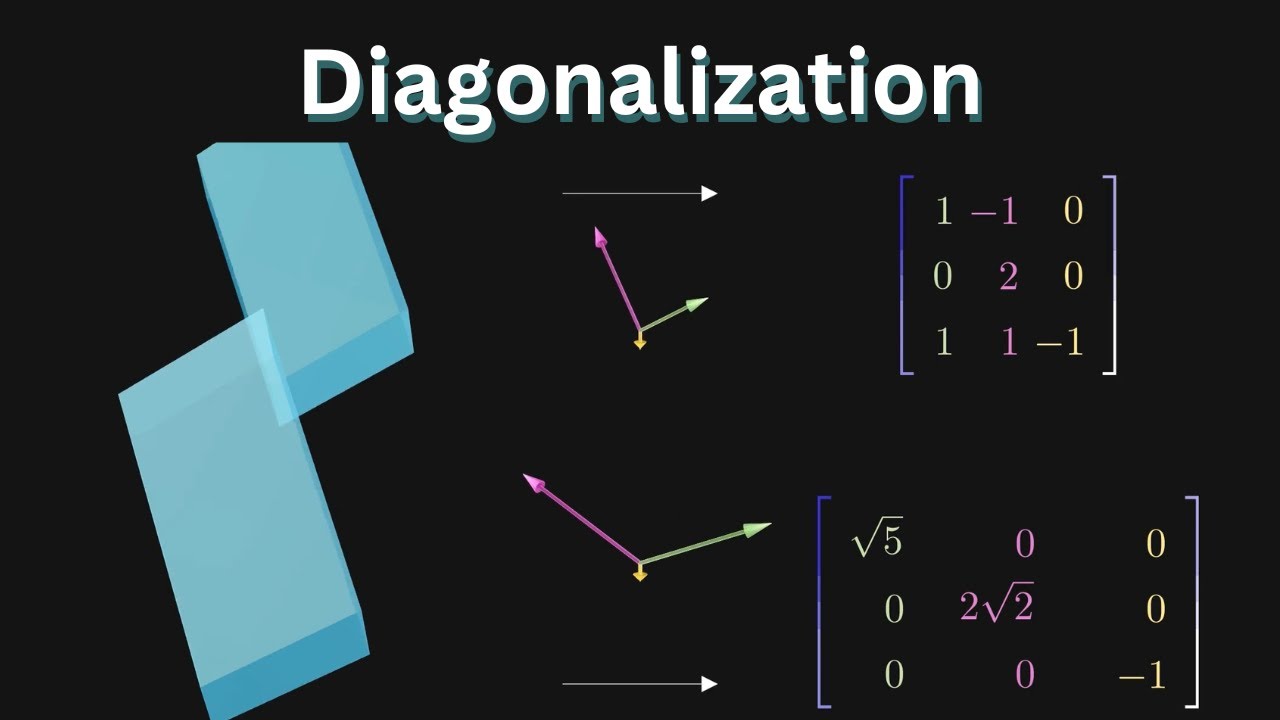
Visualizing Diagonalization

Diagonalization allows us to compute very large powers quickly, which has uses in computer science, engineering, and modeling as square matrices can represent all kinds of things.
There is a new video soon answering the question: "Can a matrix always be diagonalized?"

Made by
Nic Swanson

Follow me on Twitter for more Math related content!
@QualityMathVis

Code for the Videos: (repository work in progress)

"Tokyo Music Walker - Dawn In Tokyo" is is under a Creative Commons (CC BY-NC-SA 3.0) license.
/ @tokyomusicwalker...

[sebastiantruijens]

I am usually a silent observer of Youtube videos, but this is special. Enjoyed every second of it. Thank you for making this.

[raypanzer]

This is a very high quality math visual! Never knew my homework was interesting 👍

[rahman]

Great expalnation. The animations and visuals were amazing.
Answers:
1) The direction invariant vectors are called Eigen vectors
2)A matrix is diagonalizable if it has enough linearly independent eigen vectors to span the space
3)The diagonal entries are the eigen values. correct me if i am wrong. Thanks!

[wyboo]

there's a great book called Linear and Geometric Algebra by Alan Macdonald. while a good portion of it is about building the foundation of geometric algebra (a very clean way of unifying many parts of linear algebra by defining a new operation on vectors), the best part about the book is that it teaches linear algebra and linear transformations without much matrix usage; there's like one or two chapters covering matrices, as they are important, but most discussion of linear transformations is matrix-free. i really like it because i think matrices are so heavily tied with linear transformations that the two tools can get conflated with one another

[jonkazmaier]

HOW does this not have more views?? Best visualization of this concept I have ever seen

[spyral]

Wow, this is incredible. I must say you have done a very good job with this video, and you explained the concepts of diagonalization very concisely. Thanks!

[tune_m]

Very insightful! Question: when you read the equation at 4:27 you read it from left to right, but aren't the matrices composited from right to left?

[CrusaderGeneral]

I can watch these in a loop all dal long!

[OpPhilo]

Great video sir.
Thank you so much Sir❤

[starcrosswongyl]

Hi with regards to the PDP^-1. The P^-1 is convert to the new basis after which scale by D and then rotate back to the standard basis by P. Am i correct?

[alexmathewelt]

Fun fact: to calculate the largest power of a matrix, where the exponent still fits in 64bit unsigned long, there are only 128 Multiplications needed. Example: You want to calculate 5^14. We split the exponent in binary: 5^(2¹+2²+2³) = 5² × (5²)² × ((5²)²)² = 6.103.515.625 .
We only have to x := x², and if the current bit is on, we multiply our result with the current power, then we square x again... So to calculate powers up to about 4 Billion, u only need at most 64 multiplications. 32 for the squaring and at most 32 for the result multiplication. Since computers do not have more difficulties with larger numbers, that reduces the amount of calculations by an insane amount.

[buirabxs]

Guys how i understand we dividing some linear transformation to different steps that easier to calculate, i mean our p matrix help us to change basis and D changes sizes and P inverse ends the work, now i have question:
Is it correct to say that P realize some rotation that we need and D just change sizes????

[diamondredchannel]

Sir can you send me example of diagonalisable 5×5 matrix example

[Nalber]

I was thinking the other day what was used before analytical geometry. And then discovered synthetic geometry. I think there's a need for a balance between analytical and synthetic geometry. What do you think?
Lovely animation, btw ❤