filmov
tv
Linear Algebra 15c: The Reflection Transformation and Introduction to Eigenvalues

Показать описание
Linear Algebra 15c: The Reflection Transformation and Introduction to Eigenvalues
Reflections and projective linear algebra | Universal Hyperbolic Geometry 15 | NJ Wildberger
Linear Algebra: Reflection in any Linear Line y=ax+b
Linear transformation examples: Scaling and reflections | Linear Algebra | Khan Academy
Linear Algebra 19s: A Moment for Reflection... Eigenvalues
Linear Algebra: Basic Reflection and Projection Matrices
NEWYES Calculator VS Casio calculator
Linear Algebra 15 : Rotate & Scale Vectors
Deriving the Reflection Matrix in 2 Dimensions!
Linear Algebra Example Problems - Linear Transformations: Rotation and Reflection
Linear transformations with Matrices lesson 10 - Reflection in the line y=x
Linear Algebra, Reflection through a Line
Applications of row reduction (Gaussian elimination) I | Wild Linear Algebra A 15 | NJ Wildberger
Linear Transformations on Vector Spaces
Linear Algebra 15g: Geometric Transformation in Space, As Opposed to on the Plane
How to Find the Matrix of a Linear Transformation
Linear Algebra 15f: The Transformation of Translation
2.5 Transformations: dilations, rotations, and reflections
Reflection in the line y = x Transformation Matrix
Compose Reflections & Rotations w/ Matrix Multiplication, Inverse Transformations & Inverse ...
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Ch8Pr4: Eigenvalues and Eigenvectors of a Reflection
BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb
IIT Bombay CSE 😍 #shorts #iit #iitbombay
Комментарии
 0:20:06
0:20:06
 0:50:29
0:50:29
 0:14:33
0:14:33
 0:15:13
0:15:13
 0:10:18
0:10:18
 0:09:18
0:09:18
 0:00:14
0:00:14
 0:08:20
0:08:20
 0:12:38
0:12:38
 0:07:20
0:07:20
 0:07:05
0:07:05
 0:09:51
0:09:51
 0:41:38
0:41:38
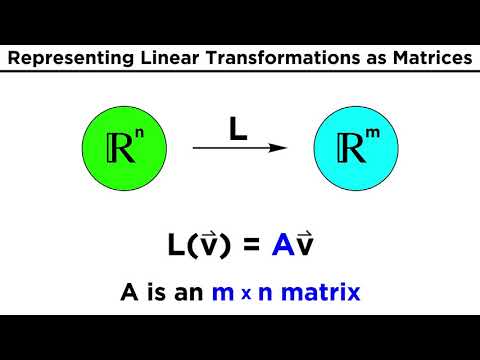 0:09:11
0:09:11
 0:17:32
0:17:32
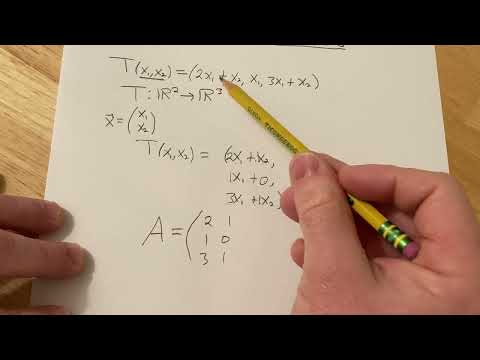 0:05:19
0:05:19
 0:03:42
0:03:42
 0:15:56
0:15:56
 0:02:15
0:02:15
 0:33:10
0:33:10
 0:13:52
0:13:52
 0:04:42
0:04:42
 0:00:15
0:00:15
 0:00:11
0:00:11