filmov
tv
Speed of light from Maxwell's equations (derivation)

Показать описание
a)Write the Maxwell’s equations and explain the significance of each
equation.
(b) Deduce the Maxwell equations for free space and determine speed of light in free space.
#maxwell'sequations #emwaves #speedoflight #maxwellandspeedoflight #gradiant #gusseslaw #divergence #curl #electricfield #magneticfield
equation.
(b) Deduce the Maxwell equations for free space and determine speed of light in free space.
#maxwell'sequations #emwaves #speedoflight #maxwellandspeedoflight #gradiant #gusseslaw #divergence #curl #electricfield #magneticfield
Why is the speed of light what it is? Maxwell equations visualized
Maxwell's Equations and the Speed of Light | Doc Physics
Classroom Aid - Maxwell's Speed of Light
Speed of light from Maxwell's equations (derivation)
Let There Be Light: Maxwell's Equation EXPLAINED for BEGINNERS
Speed of LIGHT calculated from MAXWELL equation 💡 #shorts #youtubeshorts #electrical #electronics
Deriving the speed of light from Maxwell's Equations using A-Level mathematics!
Deriving speed of light using Maxwell's equations | EM waves | Physics | Khan Academy
Physics Action at a distance 14 10 24 #Shorts #YouTube #Trending #Viral #News #Headlines
Why is the speed of light 299,792,458 m/s? (and not 300,000 km/s)
THIS inspired Einstein to develop relativity
14.10 How did Maxwell find the speed of Electromagnetic waves?
Are Maxwell's Equations Correct? - Variable Speed of Light
Physics 46 Maxwell's Equations (2 of 30) Speed of Light
Einstein on the speed of light | Cumrun Vafa and Lex Fridman
speed of light - a fundamental constant | #physics #einstein #maxwell #science #facts
Maxwell equation speed of light is constant
Maxwell's Equation plus the Derivation of the Speed of Light
What is Light? Maxwell and the Electromagnetic Spectrum
Time Dilation - Einstein's Theory Of Relativity Explained!
Maxwell's Equations for Electromagnetism Explained in under a Minute!
Why the Speed of Light is the Ultimate Speed Limit | The Physics of the Universe
Base for Special Relativity theory | Why is the speed of light constant
Electromagnetic Waves, Maxwell's Equations, Speed of Light
Комментарии
 0:13:19
0:13:19
 0:05:46
0:05:46
 0:02:32
0:02:32
 0:11:18
0:11:18
 0:10:38
0:10:38
 0:00:05
0:00:05
 0:53:26
0:53:26
 0:19:47
0:19:47
 0:17:47
0:17:47
 0:16:00
0:16:00
 0:05:07
0:05:07
 0:01:25
0:01:25
 0:22:44
0:22:44
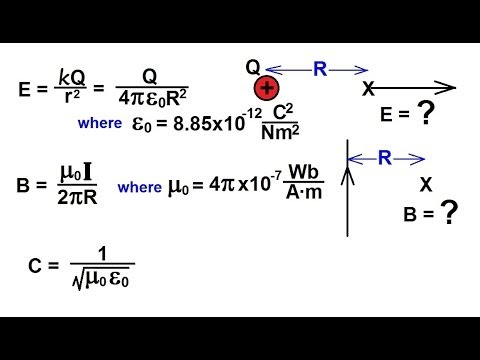 0:04:04
0:04:04
 0:06:25
0:06:25
 0:00:44
0:00:44
 0:00:10
0:00:10
 0:35:53
0:35:53
 0:03:56
0:03:56
 0:08:06
0:08:06
 0:00:59
0:00:59
 0:27:55
0:27:55
 0:09:13
0:09:13
 0:17:31
0:17:31