Calculate Final Velocity of a Chain Sliding Off A Table | Force & Energy

Показать описание

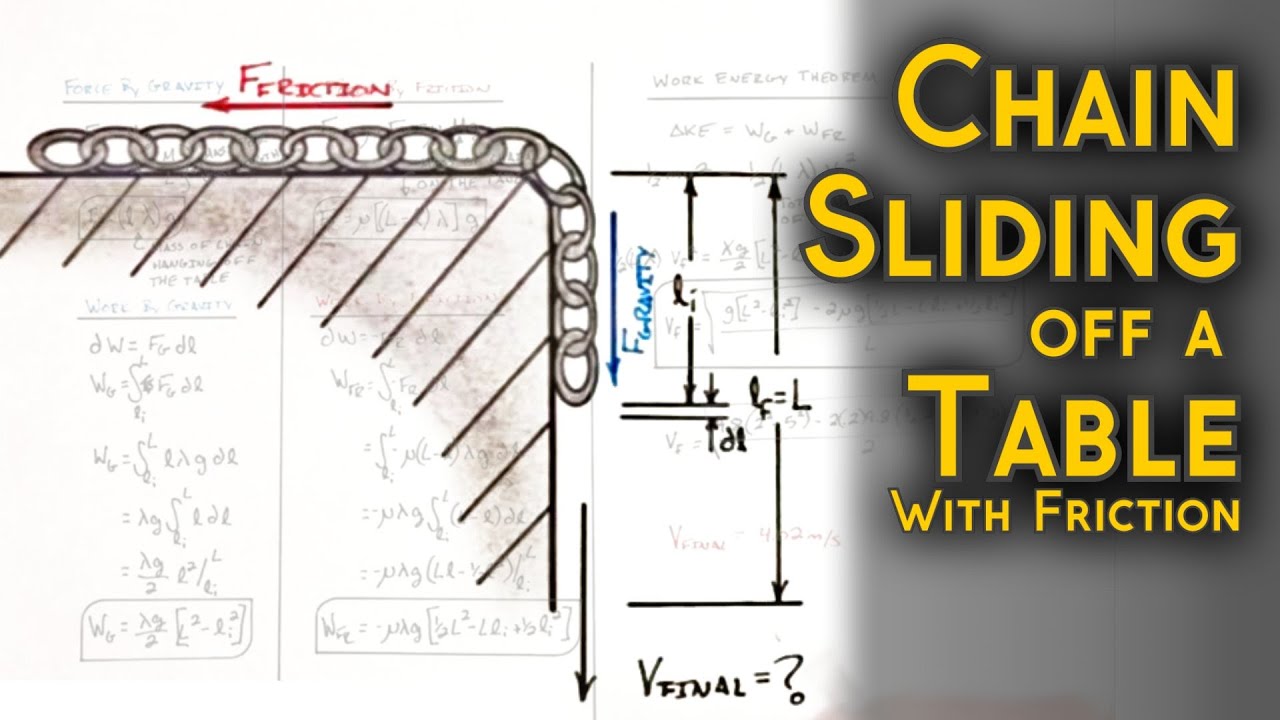
This problem is essentially an Atwood Machine, however because the hanging mass changes as the chain moves off the table. The Net Force acting on the chain is a function of position. So rather than using Newton's Laws and the kinematic equations to solve for the velocity of the chain, we will use the conservation of mechanical energy.

By coming up with equations for both the gravitational force (forward) and the friction force (backward) as functions of position, we can integrate those functions with respect to position the use the Work Energy Theorem to solve for the final Kinetic Energy of the chain.

This problem can also be solved by coming up with an equation for the net force the setting up a differential equation to relate the acceleration to the position. While this method may be simpler for some, many people seeing this problem in an introductory physics course have not taken differential equations.

This problem often comes up in AP Physics C Mechanics courses as well as introductory physics courses for scientists and engineers.