Henry Adams (5/29/20): Borsuk-Ulam theorems into higher-dimensional codomains

Title: Borsuk-Ulam theorems into higher-dimensional codomains

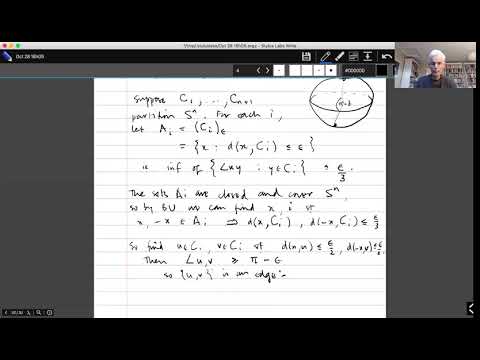
Abstract: I will describe Borsuk-Ulam theorems into higher-dimensional codomains. One formulation of the Borsuk-Ulam theorem is that any odd map from the n-dimensional sphere into Euclidean space R^n hits the origin. We generalize this result by increasing the dimension of the codomain, and by finding a small-diameter subset of the sphere whose image contains the origin in its convex hull. For example, given an odd map from the circle into R^{2k+1}, there is some subset of the circle of diameter at most 2πk/(2k+1) whose image contains the origin in its convex hull, and this diameter bound is sharp. We will pose open questions for the n-sphere, where optimal diameters are known only for odd maps of the n-sphere into R^{n+1} and R^{n+2}, and relate these questions to Schur polynomials. Joint work with Johnathan Bush and Florian Frick.

This talk was for the Rocky Mountain Algebraic Combinatorics Seminar