filmov
tv
Karnaugh Maps: Sum of Products to map, grouping and reduction explained (Intro Digital Logic Part 7)

Показать описание
Welcome to intro to digital logic part 7 karnaugh maps for sum of product expressions. In this video we will be going over how to map a sum of product Boolean expression on a karnaugh map, how to group variables plotted on the map and how to reduce the expression using a karnaugh map.
So what is the purpose of a karnaugh map… a karnaugh map is used to simplify Boolean expressions. It consists of rows of Boolean variable combinations in this case a and b and columns that consists of Boolean variable combinations in this case c and d.
The cobinations are represent as 1 and 0’s. The ones represent on or true or high states. The zeros represent off or false or low states. Recall that a Boolean variable with a line over top is equal to a zero for that variable and if it does not have a bar over top it is equal to a one
Now lets look at a sum of product formula and put it into the karnaugh map.
The first group not a and not b and not c and d can be maped and represent placing a 1 in the first row second comlum. Because this expression is represented by the first two variables 00 for a and b which is the first row and the second set of variables CD are 01 which is represented by the second column
The second group of variables can be represented by 0100 which corresponds to row 2 column 1.
Completing the same procedure for the rest of the Boolean expression we get the displayed table. You might want to pause here for a minute to take it in.Now great we have a karnaugh map for sum of product of a set of variables now what.
Well in order to reduce this we must under stand how to group variables. You can group variables if they are in adjacent cells within the map or matrix. Here is a diagram that shows all of the possible directions you can group variables.
We can group the values within the cells from side to side and up and down
For the values on the edge of the matrix we can wrap it around to the value on the other side as depicted
All together all directions that we can group look like this…
Now lets do some examples of grouping the first example we have two 1’s next to each other we group them by circling the pair
So now if we were to have another set of ones next to it would we group it like this???
No we would group it with a box around all values like this… The box around the values trump the side by side only match.
So no if you have a 3 column 2 row set of 1’s would you group it like this???
No in order to group a set of 1’s the adjacent number of 1’s must be even. So being there is 3 1’s in a row we can only group 2 of those 1’s at a time. If there were to be 4 ones in a row we could group those together. So we would group it with two 2 by 2 boxes like this.
Now lets say we have one 1 all by itself next to a box how do we group this???
We group it with the adjacent cell like so
Now lets say we have 1’s like this do we have a group anywhere???
Yes we do recall that the adjacent cells also wrap around so the grouping would look like this… The ones are grouped by wrapping around to the other side of the map or matrix.
This also applies if there is a box grouping like depicted
Now lets say you have a column of 1’s like this how would you group it like this???
No you would group the 1’s as a single column by 4 row box as depicted.
2 columns of 1’s next to eachother???
You would group it like this with one single 2 column by 4 row box.
So now how would you group this one??? Pause here and think about it…
You would group it like this… with 1 rectangle for the 2 columns and one box that wraps around the the bottom and one box that is at the bottom.
Now following the rules we learned from the previous slides how would we group the original problem…. Pause here to work it out for yourself…
It would look like this… so now you are probably thinking great I know how to group values together what is this used for?
We can use this to reduce to the minimum sum of product expression… the way we do this is by finding the variables that do not change insides each box. then we take the variables that do not change in each box and add them to eachother.
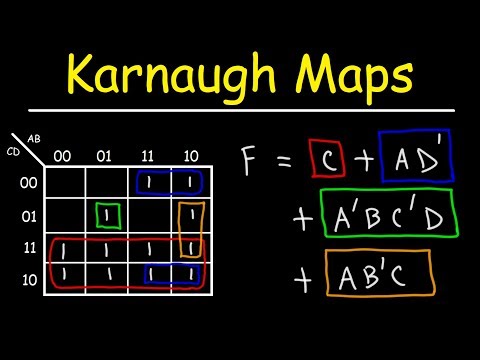
So first purple box is by itself so it remains as not a and not b and not c and d
The blue square box has all variables except for B and not D change so this is reduced down to B and not D
The orange rectangle has the variable d change so that is omitted and we are left with a and b and c.
So adding all of those boxes reduced value we get the displace equivalent minium reduced sum of product expression.
Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.
So what is the purpose of a karnaugh map… a karnaugh map is used to simplify Boolean expressions. It consists of rows of Boolean variable combinations in this case a and b and columns that consists of Boolean variable combinations in this case c and d.
The cobinations are represent as 1 and 0’s. The ones represent on or true or high states. The zeros represent off or false or low states. Recall that a Boolean variable with a line over top is equal to a zero for that variable and if it does not have a bar over top it is equal to a one
Now lets look at a sum of product formula and put it into the karnaugh map.
The first group not a and not b and not c and d can be maped and represent placing a 1 in the first row second comlum. Because this expression is represented by the first two variables 00 for a and b which is the first row and the second set of variables CD are 01 which is represented by the second column
The second group of variables can be represented by 0100 which corresponds to row 2 column 1.
Completing the same procedure for the rest of the Boolean expression we get the displayed table. You might want to pause here for a minute to take it in.Now great we have a karnaugh map for sum of product of a set of variables now what.
Well in order to reduce this we must under stand how to group variables. You can group variables if they are in adjacent cells within the map or matrix. Here is a diagram that shows all of the possible directions you can group variables.
We can group the values within the cells from side to side and up and down
For the values on the edge of the matrix we can wrap it around to the value on the other side as depicted
All together all directions that we can group look like this…
Now lets do some examples of grouping the first example we have two 1’s next to each other we group them by circling the pair
So now if we were to have another set of ones next to it would we group it like this???
No we would group it with a box around all values like this… The box around the values trump the side by side only match.
So no if you have a 3 column 2 row set of 1’s would you group it like this???
No in order to group a set of 1’s the adjacent number of 1’s must be even. So being there is 3 1’s in a row we can only group 2 of those 1’s at a time. If there were to be 4 ones in a row we could group those together. So we would group it with two 2 by 2 boxes like this.
Now lets say we have one 1 all by itself next to a box how do we group this???
We group it with the adjacent cell like so
Now lets say we have 1’s like this do we have a group anywhere???
Yes we do recall that the adjacent cells also wrap around so the grouping would look like this… The ones are grouped by wrapping around to the other side of the map or matrix.
This also applies if there is a box grouping like depicted
Now lets say you have a column of 1’s like this how would you group it like this???
No you would group the 1’s as a single column by 4 row box as depicted.
2 columns of 1’s next to eachother???
You would group it like this with one single 2 column by 4 row box.
So now how would you group this one??? Pause here and think about it…
You would group it like this… with 1 rectangle for the 2 columns and one box that wraps around the the bottom and one box that is at the bottom.
Now following the rules we learned from the previous slides how would we group the original problem…. Pause here to work it out for yourself…
It would look like this… so now you are probably thinking great I know how to group values together what is this used for?
We can use this to reduce to the minimum sum of product expression… the way we do this is by finding the variables that do not change insides each box. then we take the variables that do not change in each box and add them to eachother.
So first purple box is by itself so it remains as not a and not b and not c and d
The blue square box has all variables except for B and not D change so this is reduced down to B and not D
The orange rectangle has the variable d change so that is omitted and we are left with a and b and c.
So adding all of those boxes reduced value we get the displace equivalent minium reduced sum of product expression.
Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.
Комментарии
 0:29:44
0:29:44
 0:05:46
0:05:46
 0:07:53
0:07:53
 0:11:52
0:11:52
 0:04:26
0:04:26
 0:05:43
0:05:43
 0:06:28
0:06:28
 0:05:07
0:05:07
 1:57:03
1:57:03
 0:07:40
0:07:40
 0:21:40
0:21:40
 0:03:18
0:03:18
 0:12:31
0:12:31
 0:03:56
0:03:56
 0:02:23
0:02:23
 0:03:51
0:03:51
 0:16:01
0:16:01
 0:03:05
0:03:05
 0:00:51
0:00:51
 0:10:22
0:10:22
 0:08:49
0:08:49
 0:15:32
0:15:32
 0:10:11
0:10:11
 0:05:23
0:05:23