filmov
tv
Find Earth's Radius Using a Sunset

Показать описание
Here I show how to calculate the radius of Earth to surprising accuracy using just a sunset.
I go into theory involving Earth's rotation and derive an equation to find the radius before reviewing my results from the experiment.
0:00 - Introduction
0:10 - Utility of Sunsets
1:10 - Theory Behind Method
3:46 - Deriving the Final Radius Equation
4:44 - Further Considerations
6:20 - Processing Results
7:16 - Review, Other Methods and Summary
I go into theory involving Earth's rotation and derive an equation to find the radius before reviewing my results from the experiment.
0:00 - Introduction
0:10 - Utility of Sunsets
1:10 - Theory Behind Method
3:46 - Deriving the Final Radius Equation
4:44 - Further Considerations
6:20 - Processing Results
7:16 - Review, Other Methods and Summary
Measure the Earth’s Radius! (with this one complicated trick)
How Eratosthenes calculated the Earth's circumference
Find Earth's Radius Using a Sunset
Carl Sagan explains how Eratosthenes calculated circumference of the Earth
How Eratosthenes discovered the radius of the earth
How did Eratosthenes calculate the circumference of the Earth?
How to Measure the Earth's Radius
How do you measure the radius of the #earth? #science #roundearthbelievers #sciencetok #astronomy
Physics: Measure the radius of Earth by watching cats!
measuring the radius of earth | earth radius shorts
How Sunset Reveals the Radius of the Earth
Solvable: Calculating the Radius of Earth
Debunking Flat Earth in 45 Seconds!
Earth radius
Simple Experiment to Measure Earth's Radius 2300 years ago.
Earth's Magnetosphere Vs Sun's Heliosphere
Get smarter everyday|how to calculate earth’s🌏 radius while seeing sunset
Radius of the earth??
How Beautiful it is When the Sun is Trying to Kill Us
Measure the Radius of the Earth at Home? Checkmate Flat Earthers
How Much Water Is on Earth?🌊🤯
Earth's Magnetic Field vs Jupiter's Magnetic Field 🤫🗿
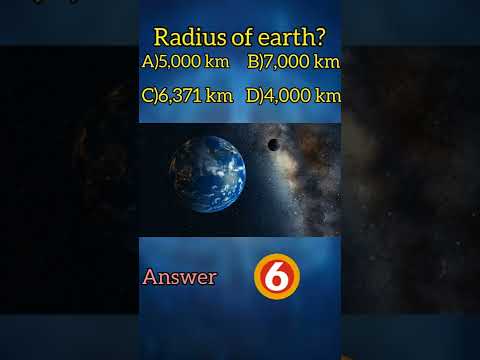
Radius of earth? game
Planet's Magnetic Field vs Sun 🤫🗿 #shorts #space #sun
Комментарии
 0:27:31
0:27:31
 0:02:02
0:02:02
 0:09:31
0:09:31
 0:02:14
0:02:14
 0:04:20
0:04:20
 0:01:36
0:01:36
 0:10:36
0:10:36
 0:01:01
0:01:01
 0:05:12
0:05:12
 0:00:35
0:00:35
 0:19:32
0:19:32
 0:00:32
0:00:32
 0:00:46
0:00:46
 0:00:13
0:00:13
 0:00:55
0:00:55
 0:00:33
0:00:33
 0:11:35
0:11:35
 0:00:37
0:00:37
 0:00:33
0:00:33
 0:00:56
0:00:56
 0:00:19
0:00:19
 0:00:25
0:00:25
 0:00:14
0:00:14
 0:00:31
0:00:31